
 ШчЭМЃЎХзЮяЯпy=x2+bx+cгыyжсНЛгкЕуCЃЈ0ЃЌ3ЃЉЃЌгыxжсНЛгкAЃЌBСНЕуЃЌAЕудкЖдГЦжсЕФзѓВрЃЌBЕуЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЎ
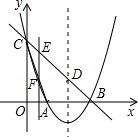
ШчЭМЃЎХзЮяЯпy=x2+bx+cгыyжсНЛгкЕуCЃЈ0ЃЌ3ЃЉЃЌгыxжсНЛгкAЃЌBСНЕуЃЌAЕудкЖдГЦжсЕФзѓВрЃЌBЕуЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЎЗжЮі ЃЈ1ЃЉНЋЕуCЃЈ0ЃЌ3ЃЉЁЂBЃЈ3ЃЌ0ЃЉДњШыХзЮяЯпЕФНтЮіЪНПЩЧѓЕУbЁЂcЕФжЕЃЌДгЖјЕУЕНХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉСЌНгADЃЎЯШЧѓЕУХзЮяЯпЕФЖдГЦжсЗНГЬЃЌШЛКѓРћгУХзЮяЯпЕФЖдГЦадЧѓЕУЕуAЕФзјБъЃЌНгЯТРДЃЌгЩЕуBКЭЕуCЕФзјБъЧѓЕУжБЯпBCЕФНтЮіЪНЃЌдйЧѓЕУЕуDЕФзјБъЃЌзюКѓвРОнSЁїADC=SЁїBAC-SЁїABDЧѓНтМДПЩЃЛ
ЃЈ3ЃЉЕБЁЯDFE=90ЁуЪБЃЌПЩЧѓЕУЕуFЕФзнзјБъЮЊ1ЃЌНЋy=1ДњШыХзЮяЯпЕФНтЮіЪНПЩЧѓЕУЕуFКЭFЁфЕФКсзјБъЃЌШЛКѓгЩПЩЧѓЕУЕуEКЭЕуEЁфЕФзјБъЃЌЕБЁЯEDF=90ЁуЪБЃЌПЩЯШЧѓЕУDFЕФНтЮіЪНЃЌШЛКѓНЋжБЯпDFЕФНтЮіЪНгыХзЮяЯпЕФНтЮіЪНСЊСЂЧѓЕУЕуFКЭЕуFЁфЕФзјБъЃЌШЛКѓгЩПЩЧѓЕУЕуEКЭЕуEЁфЕФзјБъ
НтД№ НтЃКЃЈ1ЃЉЁпНЋЕуCЃЈ0ЃЌ3ЃЉЁЂBЃЈ3ЃЌ0ЃЉДњШыХзЮяЯпЕФНтЮіЪНЕУЃК$\left\{\begin{array}{l}{9+3b+c=0}\\{c=3}\end{array}\right.$ЃЌНтЕУЃКb=-4ЃЌc=3ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊy=x2-4x+3ЃЎ
ЃЈ2ЃЉШчЭМ1ЫљЪОЃЌСЌНгADЃЎ
Ёпx=-$\frac{b}{2a}$=-$\frac{-4}{2ЁС1}$=2ЃЌBЃЈ3ЃЌ0ЃЉЃЌ
ЁрAЃЈ1ЃЌ0ЃЉЃЎ
ЁрAB=2ЃЎ
ЩшжБЯпBCЕФНтЮіЪНЮЊy=kx+bЃЎ
ЁпНЋCЃЈ0ЃЌ3ЃЉЁЂBЃЈ3ЃЌ0ЃЉДњШыЕУЃК$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$ЃЌНтЕУЃКk=-1ЃЌb=3ЃЌ
ЁржБЯпBCЕФНтЮіЪНЮЊy-x+3ЃЎ
ЁпНЋx=2ДњШыЕУЃКy=-2+3=1ЃЌ
ЁрDЃЈ2ЃЌ1ЃЉЃЎ
ЁрDG=1ЃЎ
ЁпSЁїADC=SЁїBAC-SЁїABDЃЌ
ЁрSЁїADC=$\frac{1}{2}$BA•OC-$\frac{1}{2}$AB•DE=$\frac{1}{2}$ЁС2ЁС3-$\frac{1}{2}$ЁС2ЁС1=2ЃЎ
ЃЈ3ЃЉШчЭМ2ЫљЪОЃКЕБЁЯDFE=90ЁуЪБЃЎ
ЁпEFЁЮOCЃЌ
ЁрЁЯDEF=ЁЯBCOЃЎ
ЁпЁЯCOB=ЁЯEFD=90ЁуЃЌ
ЁрЁїEFDЁзЁїCOBЃЎ
ЁрЁЯEDF=ЁЯCBOЃЎ
ЁрDFЁЮOBЃЎ
ЁрЕуFЕФзнзјБъЮЊ1ЃЎ
НЋy=1ДњШыХзЮяЯпЕФНтЮіЪНЕУЃЛx2-4x+3=1ЃЌНтЕУЃКx1=2-$\sqrt{2}$ЃЌx2=2$+\sqrt{2}$ЃЌ
ЁпНЋx=2-$\sqrt{2}$ДњШыy=-x+3ЕУЃЛy=$\sqrt{2}$+1ЃЌ
ЁрEЃЈ2-$\sqrt{2}$ЃЌ$\sqrt{2}$+1ЃЉЃЎ
ЁпНЋx=2$+\sqrt{2}$ДњШыy=-x+3ЕУЃЛy=1-$\sqrt{2}$ЃЌ
ЁрEЁфЕФзјБъЮЊЃЈ2+$\sqrt{2}$ЃЌ1-$\sqrt{2}$ЃЉЃЎ
ШчЭМ3ЫљЪОЃКЕБЁЯEDF=90ЁуЪБЃЌ
ЁпЁЯDEF=ЁЯBCOЃЌЁЯEDF=ЁЯCOB=90ЁуЃЌ
ЁрЁїEDFЁзЁїCOBЃЎ
ЁпDFЁЭOBЃЌ
ЁржБЯпDFЕФвЛДЮЯюЯЕЪ§ЮЊ1ЃЎ
ЩшDFЕФНтЮіЪНЮЊy=x+bЃЌНЋDЃЈ2ЃЌ1ЃЉДњШыЕУ2+b=1ЃЌНтЕУb=-1ЃЌ
ЁржБЯпDFЕФНтЮіЪНЮЊy=x-1ЃЎ
НЋy=x-1гыy=x2-4x+3СЊСЂЃЌНтЕУЃКx1=1ЃЌx2=4ЃЎ
ЁпНЋx=1ДњШыy=-x+3ЕУy=2ЃЌ
ЁрEЃЈ1ЃЌ2ЃЉЃЎ
НЋx=4ДњШыy=-x+3ЕУЃКy=-1ЃЌ
ЁрEЁфЃЈ4ЃЌ-1ЃЉЃЎ
злЩЯЫљЪіЃЌЕуEЕФзјБъЮЊЃЈ2-$\sqrt{2}$ЃЌ$\sqrt{2}$+1ЃЉЛђЃЈ2+$\sqrt{2}$ЃЌ1-$\sqrt{2}$ЃЉЛђЃЈ1ЃЌ2ЃЉЛђЃЈ4ЃЌ-1ЃЉЃЎ
ЕуЦР БОЬтжївЊПМВщЕФЪЧЖўДЮКЏЪ§ЕФзлКЯгІгУЃЌНтД№БОЬтжївЊгІгУСЫД§ЖЈЯЕЪ§ЗЈЧѓЖўДЮКЏЪ§ЁЂвЛДЮКЏЪ§ЕФНтЮіЪНЁЂШ§НЧаЮЕФУцЛ§ЙЋЪНЁЂЯрЫЦШ§НЧаЮЕФХаЖЈКЭаджЪЃЌвРОнЬтвтЛГіЗћКЯЬтвтЕФЭМаЮЪЧНтЬтЕФЙиМќЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
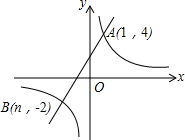 ШчЭМЃЌвбжЊЗДБШР§КЏЪ§y=$\frac{m}{x}$ЕФЭМЯѓгывЛДЮКЏЪ§y=ax+bЕФЭМЯѓЯрНЛгкЕуAЃЈ1ЃЌ4ЃЉКЭЕуBЃЈnЃЌ-2ЃЉЃЎ
ШчЭМЃЌвбжЊЗДБШР§КЏЪ§y=$\frac{m}{x}$ЕФЭМЯѓгывЛДЮКЏЪ§y=ax+bЕФЭМЯѓЯрНЛгкЕуAЃЈ1ЃЌ4ЃЉКЭЕуBЃЈnЃЌ-2ЃЉЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ШєСНЯрЕШЕФНЧгавЛБпЦНааЃЌдђСэвЛБпвВЛЅЯрЦНаа | |
| BЃЎ | СНЬѕжБЯпЯрНЛЃЌЫљГЩЕФСНзщЖдЖЅНЧЕФЦНЗжЯпЛЅЯрДЙжБ | |
| CЃЎ | СНЬѕЦНааЯпБЛЕкШ§ЬѕжБЯпЫљНиЃЌЭЌХдФкНЧЕФЦНЗжЯпЛЅЯрДЙжБ | |
| DЃЎ | ОЙ§жБЯпЭтвЛЕуЃЌгаЧвжЛгавЛЬѕжБЯпгывбжЊжБЯпЦНаа |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
 ФГЛЌбЉГЁОйАьБљбЉМЮФъЛЊЛюЖЏЃЌВЩгУжБЩ§ЛњКНХФММЪѕХФЩуЛюЖЏЪЂПіЃЎШчЭМЃЌЭЈЙ§жБЩ§ЛњЕФОЕЭЗCЙлВтЕНЫЎЦНбЉЕРвЛЖЫAДІЕФИЉНЧЮЊ30ЁуЃЌСэвЛЖЫBДІЕФИЉНЧЮЊ45ЁуЃЎШєжБЩ§ЛњОЕЭЗCДІЕФИпЖШCDЮЊ300УзЃЌЕуAЁЂDЁЂBдкЭЌвЛжБЯпЩЯЃЌдђбЉЕРABЕФГЄЖШЮЊЃЈЁЁЁЁЃЉ
ФГЛЌбЉГЁОйАьБљбЉМЮФъЛЊЛюЖЏЃЌВЩгУжБЩ§ЛњКНХФММЪѕХФЩуЛюЖЏЪЂПіЃЎШчЭМЃЌЭЈЙ§жБЩ§ЛњЕФОЕЭЗCЙлВтЕНЫЎЦНбЉЕРвЛЖЫAДІЕФИЉНЧЮЊ30ЁуЃЌСэвЛЖЫBДІЕФИЉНЧЮЊ45ЁуЃЎШєжБЩ§ЛњОЕЭЗCДІЕФИпЖШCDЮЊ300УзЃЌЕуAЁЂDЁЂBдкЭЌвЛжБЯпЩЯЃЌдђбЉЕРABЕФГЄЖШЮЊЃЈЁЁЁЁЃЉ| AЃЎ | 300Уз | BЃЎ | 150$\sqrt{2}$Уз | CЃЎ | 900Уз | DЃЎ | ЃЈ300$\sqrt{3}$+300ЃЉУз |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com