
如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.
(1) 证明:∠BAC=∠DAC,∠AFD=∠CFE;
(2) 若AB∥CD,试证明四边形ABCD是菱形;
(3) 在(2)的条件下,试确定E点的位置,使∠EFD=∠BCD,并说明理由.

【解析】
(1) ∵AB=AD,CB=CD,AC=AC,
∴△ABC≌△ADC.
∴∠BAC =∠DAC.
∵ AB=AD,∠BAF =∠DAF,AF=AF.
∴△ABF≌△ADF.
∴∠AFB=∠AFD.
又∵∠CFE =∠AFB,
∴∠AFD=∠CFE.
∴∠BAC=∠DAC,∠AFD=∠CFE.
(2) ∵AB∥CD,
∴∠BAC=∠ACD.
又∵∠BAC=∠DAC,
∴∠BAC=∠ACD.
∴∠DAC=∠ACD.
∴AD=CD,
∵AB=AD , CB=CD,
∴AB=CB=CD=AD.
∴四边形ABCD是菱形.
(3)当BE⊥CD时,∠EFD=∠BCD.理由:
∵四边形ABCD为菱形,
∴BC=CD,∠BCF=∠DCF.
又∵CF为公共边,
∴△BCF≌△DCF.
∴∠CBF=∠CDF,
∵BE⊥CD,
∴∠BEC =∠DEF=90°.
∴∠EFD =∠BCD.
【解析】
(1)利用已知条件和公共边,证得△ABC≌△ADC,即可证明∠BAC=∠DAC;再证明△ABF≌△ADF,得到∠AFB=∠AFD,再利用对顶角相等,易知结论;(2)有平行线的性质和(1)中结论,易知∠DAC=∠ACD,所以AD=CD,进而证得AB=CB=CD=AD,即可证明结论;(3)当BE⊥CD时,有(2)可知BC=CD ,∠BCF=∠DCF,利用△BCF≌△DCF证得∠CBF=∠CDF,再利用等角的余角相等即可证明结论∠EFD =∠BCD.


 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源:青岛版八年级下6.3特殊的平行四边形 题型:选择题
如图,在菱形ABCD中,已知∠A=60°,AB=5,则△ABD的周长是( )

A.10 B.12 C.15 D.20
查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.3特殊的平行四边形 题型:选择题
如图,正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰三角形有( )

A.4个 B.6个 C.8个 D.10个
查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.3特殊的平行四边形 题型:选择题
菱形具有而矩形不一定具有的性质是( )
A.对角线互相垂直
B.对角线相等
C.对角线互相平分
D.对角互补
查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.3特殊的平行四边形 题型:填空题
如图,在Rt△ABC中,∠C=90°,DE垂直平分AC,DF⊥BC,当△ABC满足条件_______时,四边形DECF是正方形. (要求:①不再添加任何辅助线,②只需填一个符合要求的条件)

查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.3特殊的平行四边形 题型:填空题
如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC、BD相交于点O,点E在AB上且BE=BO,则∠BEO=_______度.

查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.4三角形的中位线 题型:选择题
如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5,CD=3,则EF的长是( )

A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.4三角形的中位线 题型:解答题
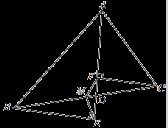
如图,在△ABC中(AB≠AC),M为BC的中点,AD平分∠BAC交BC于D,BE⊥AD于E,CF⊥AD于F,求证:ME=MF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com