练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，AB∥CD，E，F分别为AC，BD的中点，若AB=5，CD=3，则EF的长是（ ）

    A．4 B．3 C．2 D．1

     

     

     

    D

     

    【解析】

    连接DE并延长交AB于H，由已知条件可判定△DCE≌△HAE，利用全等三角形的性质可得DE=HE，进而得到EF是三角形DHB的中位线，利用中位线性质定理即可求出EF的长．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：青岛版八年级下6.2平行四边形的判定 题型：解答题

    如图，AB∥CD，AB=CD，点E、F在BC上，且BE=CF．
    （1）求证：△ABE≌△DCF；
    （2）试证明：以A、F、D、E为顶点的四边形是平行四边形．

     

     

    查看答案和解析>>

    科目：初中数学 来源：青岛版八年级下6.3特殊的平行四边形 题型：解答题

    如图，在四边形ABCD中，AB=AD，CB=CD，E是CD上一点，BE交AC于F，连接DF．

    (1) 证明：∠BAC=∠DAC，∠AFD=∠CFE；

    (2) 若AB∥CD，试证明四边形ABCD是菱形；

    (3) 在(2)的条件下，试确定E点的位置，使∠EFD=∠BCD，并说明理由．

     

     

    查看答案和解析>>

    科目：初中数学 来源：青岛版八年级下6.3特殊的平行四边形 题型：选择题

    如图，在△ABC中，AB=3，AC=4，BC=5，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，则EF的最小值为（ ）

    A．2 B．2.2 C．2.4 D．2.5

     

     

     

    查看答案和解析>>

    科目：初中数学 来源：青岛版八年级下6.3特殊的平行四边形 题型：解答题

    已知：如图，在△ABC中，D是AC的中点，E是线段BC延长线上一点，过点A作BE的平行线与线段ED的延长线交于点F，连接AE，CF．
    （1）求证：AF=CE；
    （2）若AC=EF，试判断四边形AFCE是什么样的四边形，并证明你的结论．

     

     

    查看答案和解析>>

    科目：初中数学 来源：青岛版八年级下6.4三角形的中位线 题型：选择题

    如图，D，E分别为△ABC的AC，BC边的中点，将此三角形沿DE折叠，使点C落在AB边上的点P处．若∠CDE=48°，则∠APD等于（ ）

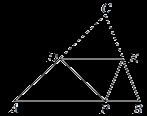
    A．42° B．48° C．52° D．58°

     

     

     

    查看答案和解析>>

    科目：初中数学 来源：青岛版八年级下6.4三角形的中位线 题型：填空题

    已知：如图，△ABC三边的中点分别为D、E、F，如果AB=6cm，AC=8cm，BC=10cm，那么△DEF的周长是_______cm．

     

     

    查看答案和解析>>

    科目：初中数学 来源：青岛版八年级下7.1算术平方根 题型：选择题

    3的算术平方根是（ ）

    A．3 B．-3 C．± D．

     

     

    查看答案和解析>>

    科目：初中数学 来源：青岛版八年级下7.2勾股定理 题型：选择题

    已知△ABC中，AB=17，AC=10，BC边上的高AD=8，则边BC的长为（ ）

    A．21 　 B．15　 C．6 　D．以上答案都不对

     

     

    查看答案和解析>>

    同步练习册答案