
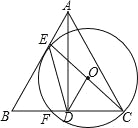
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,E为边AB上一点,ED=CD,以CE为直径作⊙O,交BC于点F.
(1)求证:AB与⊙O相切;
(2)若DF=1,DC=3,求AE的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)根据等腰三角形的性质,由AB=AC,AD⊥BC得到BD=CD,则可判断OD为△BCE的中位线,所以OD∥BE,再根据等腰三角形的性质,由DE=DC,OE=OC得到DO⊥CE,则BE⊥CE,于是根据切线的性质可判断AB与⊙O相切;
(2)连结EF,如图,根据圆周角定理得∠EFC=90°,在Rt△DEF中利用勾股定理计算出EF=2![]() ,再在Rt△BEF中利用勾股定理计算出BE=2
,再在Rt△BEF中利用勾股定理计算出BE=2![]() ,然后根据平行线分线段成比例定理可求出AE的长.
,然后根据平行线分线段成比例定理可求出AE的长.
试题解析:(1)∵AB=AC,AD⊥BC,
∴BD=CD,
∵OE=OC,
∴OD为△BCE的中位线,
∴OD∥BE,
∵DE=DC,OE=OC,
∴DO⊥CE,
∴BE⊥CE,
∴AB与⊙O相切;
(2)连结EF,如图,
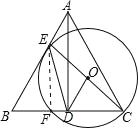
∵CE为⊙O的直径,
∴∠EFC=90°,
在Rt△DEF中,∵DE=DC=3,DF=1,
∴EF=![]() ,
,
∵DB=DC=3,
∴BF=BD-DF=3-1=2,
在Rt△BEF中,∵EF=2![]() ,BF=2,
,BF=2,
∴BE=![]() ,
,
∵EF∥AD,
∴![]() ,即
,即![]() ,
,
∴AE=![]() .
.


科目:初中数学 来源: 题型:
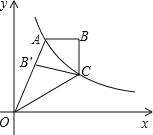
【题目】如图,双曲线y=![]() (x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴.将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则四边形OABC的面积是 .
(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴.将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则四边形OABC的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
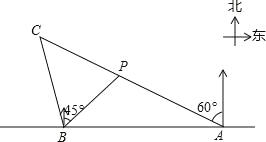
【题目】如图,在笔直的海岸线l上有A、B两个观测站,A在B的正东方向,AB=(![]() +1)km,小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°方向.
+1)km,小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°方向.
(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到达点C处,此时,从B测得小船在北偏西15°的方向,求点C与点B之间的距离.(友情提示:结果都保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)…根据这个规律,第2016个点的坐标为( )
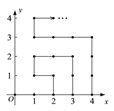
A(45,9) B(45,13) C(45,22) D(45,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】麒麟区是云南省曲靖市政府所在地,位于云南省东部,滇东高原中部,南盘江上游,截止2018年末麒麟区有常住人口约76万人,76万这个数字用科学记数法表示为( )
A. 0.76×106B. 7.6×105C. 76×104D. 7.6×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程x2+px+q=0,甲同学因为看错了常数项,解得的根是6,-1;乙同学看错了一次项,解得的根是-2,-3,则原方程为_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com