
【题目】如图,已知一次函数![]() 的图象与x轴、y轴分别交于A、B两点,且与反比例函数
的图象与x轴、y轴分别交于A、B两点,且与反比例函数![]() 的图象在第一象限交于C点,CD垂直与x轴,垂足为D.若OA=OB=OD=1,
的图象在第一象限交于C点,CD垂直与x轴,垂足为D.若OA=OB=OD=1,
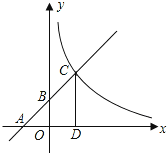
(1)求点A,B,D的坐标;
(2)求一次函数和反比例函数的解析式。
【答案】(1)A(-1,0),B(0,1),D(1,0);(2)一次函数的解析式为y=x+1.反比例函数的解析式为y=![]() .
.
【解析】
试题(1)根据OA=OB=OD=1和各坐标轴上的点的特点易得到所求点的坐标;
(2)将A、B两点坐标分别代入y=kx+b,可用待定系数法确定一次函数的解析式,由C点在一次函数的图象上可确定C点坐标,将C点坐标代入y=![]() 可确定反比例函数的解析式.
可确定反比例函数的解析式.
试题解析:(1)∵OA=OB=OD=1,
∴点A、B、D的坐标分别为A(-1,0),B(0,1),D(1,0);
(2)∵点A、B在一次函数y=kx+b(k≠0)的图象上,
∴![]() ,
,
解得![]() ,
,
∴一次函数的解析式为y=x+1.
∵点C在一次函数y=x+1的图象上,且CD⊥x轴,
∴点C的坐标为(1,2),
又∵点C在反比例函数y=![]() (m≠0)的图象上,
(m≠0)的图象上,
∴m=2;
∴反比例函数的解析式为y=![]() .
.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了![]() ,
,![]() 两种型号的空气净化器,已知一台
两种型号的空气净化器,已知一台![]() 型空气净化器的进价比一台
型空气净化器的进价比一台![]() 型空气净化器的进价多300元,用7500元购进
型空气净化器的进价多300元,用7500元购进![]() 型空气净化器和用6000元购进
型空气净化器和用6000元购进![]() 型空气净化器的台数相同.
型空气净化器的台数相同.
(1)求一台![]() 型空气净化器和一台
型空气净化器和一台![]() 型空气净化器的进价各为多少元?
型空气净化器的进价各为多少元?
(2)在销售过程中,![]() 型空气净化器因为净化能力强,噪声小而更受消费者的欢迎.商社电器计划
型空气净化器因为净化能力强,噪声小而更受消费者的欢迎.商社电器计划![]() 型净化器的进货量不少于20台且是
型净化器的进货量不少于20台且是![]() 型净化器进货量的三倍,在总进货款不超过5万元的前提下,试问有多少种进货方案?
型净化器进货量的三倍,在总进货款不超过5万元的前提下,试问有多少种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“均衡教育大检查”,县委县府对通往某偏远学校的一段全长为1200 米的道路进行了改造,铺设草油路面.铺设400 米后,为了尽快完成道路改造,后来每天的工作效率比原计划提高25%,结果共用13天完成道路改造任务.
(1)求原计划每天铺设路面多少米;
(2)若承包商原来每天支付工人工资为1500元,提高工作效率后每天支付给工人的工资增长了20%,完成整个工程后承包商共支付工人工资多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家,其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上,根据图中提供的信息,下列说法正确的是( )
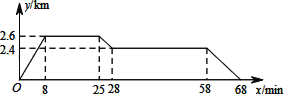
A.食堂离小明家2.4km
B.小明在图书馆呆了20min
C.小明从图书馆回家的平均速度是0.04km/min
D.图书馆在小明家和食堂之间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形纸片ABCD中,AB=12厘米,折叠纸片,使得点A落在CD边上的点P处,折痕为MN,点M、N分别在边AD、AB上,当点P恰好是CD边的中点时,点N与点B重合,若在折叠过程中NP=NC,则PD=_____.
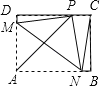
查看答案和解析>>
科目:初中数学 来源: 题型:
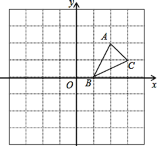
【题目】方格纸中的每个小方格都是边长为1个单位的正方形,建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(3,1).
(1)画出△ABC关于y轴对称的△A1B1C1
(2)将△A1B1C1向下平移3个单位后得到△A2B2C2,画出平移后的△A2B2C2,并写出顶点B2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
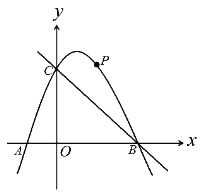
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点, 与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0))。点P是抛物线上一个动点,且在直线BC的上方.
的图象与x轴交于A、B两点, 与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0))。点P是抛物线上一个动点,且在直线BC的上方.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形![]() ,那么是否存在点P,使四边形
,那么是否存在点P,使四边形![]() 为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,使△BPC的面积最大,求出点P的坐标和△BPC的面积最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图点A(1,1),B(2,﹣3),点P为x轴上一点,当|PA﹣PB|最大时,点P的坐标为( )

A. (﹣1,0) B. (![]() ,0) C. (
,0) C. (![]() ,0) D. (1,0)
,0) D. (1,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com