
【题目】某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.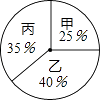
(1)分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,三人中谁的得分最高?
【答案】
(1)解:甲民主评议的得分是:
200×25%=50(分);
乙民主评议的得分是:
200×40%=80(分);
丙民主评议的得分是:
200×35%=70(分).
(2)解:甲的成绩是:
(75×4+93×3+50×3)÷(4+3+3)
=729÷10
=72.9(分)
乙的成绩是:
(80×4+70×3+80×3)÷(4+3+3)
=770÷10
=77(分)
丙的成绩是:
(90×4+68×3+70×3)÷(4+3+3)
=774÷10
=77.4(分)
∵77.4>77>72.9,
∴丙的得分最高.
【解析】(1)根据百分数乘法的意义,分别用200乘以三人的得票率,求出三人民主评议的得分各是多少即可.(2)首先根据加权平均数的计算方法列式计算,分别求出三人的得分各是多少;然后比较大小,判断出三人中谁的得分最高即可.


科目:初中数学 来源: 题型:
【题目】在由6个边长为1的小正方形组成的方格中:
(1)如图(1),A、B、C是三个格点(即小正方形的顶点),判断AB与BC的关系,并说明理由;
(2)如图(2),连结三格和两格的对角线,求∠α+∠β的度数(要求:画出示意图并给出证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生体质情况,从各年级随机抽取部分学生进行体能测试,每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级.统计员在将测试数据绘制成图表时发现,优秀漏统计![]() 人,良好漏统计
人,良好漏统计![]() 人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题:
人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题:
(1)填写统计表.
(2)根据调整后数据,补全条形统计图.
(3)若该校共有学生![]() 人,请你估算出该校体能测试等级为“优秀”的人数.
人,请你估算出该校体能测试等级为“优秀”的人数.
学生体能测试成绩各等次人数统计表
体能等级 | 调整前人数 | 调整后人数 |
优秀 |
| |
良好 |
| |
及格 |
| |
不及格 |
| |
合计 |
|
学生体能测试成绩各等次人数统计图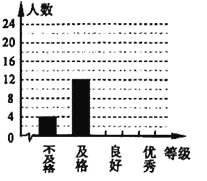
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间(如图),![]() ,
,![]() ,从三角板的刻度可知
,从三角板的刻度可知![]() ,小聪很快就知道了砌墙砖块的厚度的平方(每块砖的厚度相等)为________
,小聪很快就知道了砌墙砖块的厚度的平方(每块砖的厚度相等)为________![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( ) 
A.![]() a2
a2
B.![]() a2
a2
C.![]() a2
a2
D.![]() a2
a2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不要求写出画法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料并解决有关问题:
我们知道:|x|= .现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:
.现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:
①x<﹣1;②﹣1≤x<2;③x≥2.
从而化简代数式|x+1|+|x﹣2|可分以下3种情况:
①当x<﹣1时,原式=﹣(x+1)﹣(x﹣2)=﹣2x+1;
②当﹣1≤x<2时,原式=x+1﹣(x﹣2)=3;
③当x≥2时,原式=x+1+x﹣2=2x﹣1.综上讨论,原式= .
.
通过以上阅读,请你解决以下问题:
(1)化简代数式|x+2|+|x﹣4|.
(2)求|x﹣1|﹣4|x+1|的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)


(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正![]() 边形ABCD……X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD……X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com