
����Ŀ��
��1����ͼ1����������ABCD�У�M��BC�ߣ������˵�B��C��������һ�㣬P��BC�ӳ�����һ�㣬N����DCP��ƽ������һ�㣮����AMN=90������֤��AM=MN��
�������һ��֤����˼·���������һ˼·֤����Ҳ����ѡ������ķ���֤����
֤�����ڱ�AB�Ͻ�ȡAE=MC����ME��������ABCD�У���B=��BCD=90����AB=BC��
���NMC=180������AMN����AMB=180������B����AMB=��MAB=��MAE��
����������������µ�֤�����̣�


��2��������1���е���������ABCD����Ϊ����������ABC������ͼ2����N����ACP��ƽ������һ�㣬����AMN=60��ʱ������AM=MN�Ƿ�������˵�����ɣ�
��3��������1���е���������ABCD����Ϊ����![]() ����ABCD����X���������������룺����AMN= ��ʱ������AM=MN��Ȼ��������ֱ��д���𰸣�����Ҫ֤����
����ABCD����X���������������룺����AMN= ��ʱ������AM=MN��Ȼ��������ֱ��д���𰸣�����Ҫ֤����
���𰸡�
��1��֤����
��2��������
��3��![]()
���������⣺��1����AE=MC����BE=BM�� ���BEM=��EMB=45���� ���AEM=135����
��CNƽ����DCP�����PCN=45�������AEM=��MCN=135��
����AEM����MCN�У���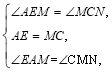 ���AEM�ա�MCN����AM=MN
���AEM�ա�MCN����AM=MN
��2����Ȼ������
�ڱ�AB�Ͻ�ȡAE=MC������ME
�ߡ�ABC�ǵȱ������Σ�
��AB=BC����B=��ACB=60����
���ACP=120����
��AE=MC����BE=BM
���BEM=��EMB=60��
���AEM=120����
��CNƽ����ACP�����PCN=60����
���AEM=��MCN=120��
�ߡ�CMN=180������AMN����AMB=180������B����AMB=��BAM
���AEM����MCN����AM=MN
��3��![]()


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2��2��m+1��x+m��m+2��
��1����֤������mΪ�κ�ʵ�����ú���ͼ����x����������֮��ľ���Ϊ��ֵ��
��2�����ú���ͼ��ĶԳ���Ϊֱ��x=2��������κ�������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ڼ䣬ѧУ��֯ѧ��ȥij�������棬��������˵����������ӵ�һ����ʦ����ȫƱ����ѧ�����ܰ���Ż����� ��������˵���������˰�ȫƱ�۵������Ż�������֪ȫƱ��ΪaԪ��ѧ����x�ˣ�������ʦ��1�ˣ�
(1)���ú�a��x��ʽ�ӱ�ʾ�ס���������ķ��ã�
(2)����50��ѧ���μӱ��λ������Ϊ����ѡ��һ�Ҹ��Żݵ������磮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ͬ����С�ĺ�ɫ���Ӱڷ���������εı��ϣ����������Ĺ��ɰ���ȥ�����10��n�Ǵ���0����������ͼ����Ҫ��ɫ���ӵĸ�����_______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
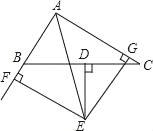
����Ŀ����ͼ���ڡ�ABC�У�BC���ϵĴ�ֱƽ����DE���BAC��ƽ���߽��ڵ�E��EF��AB��AB���ӳ����ڵ�F��EG��AC�ڵ�G��
��֤����1��BF��CG��
��2��AB+AC��2AF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������OABC�ı�OA�������ϣ�OΪԭ�㣬������OABC�����Ϊ12��OC�߳�Ϊ3.

(1)�����ϵ�A��ʾ����Ϊ________��
(2)��������OABC������ˮƽ�ƶ����ƶ���ij����μ�ΪO��A��B��C�����ƶ���ij�����O��A��B��C����ԭ������OABC�ص�����(��ͼ2����Ӱ����)�������ΪS.
�ٵ�Sǡ�õ���ԭ������OABC�����һ��ʱ�������ϵ�A����ʾ�����Ƕ��٣�
�� �����A���ƶ�����AA����x.
�� ����)��S��4ʱ����x��ֵ��
�� ����)DΪ�߶�AA�����е㣬��E���߶�OO���ϣ���OE��![]() OO��������D��E����ʾ������Ϊ�෴��ʱ����x��ֵ��
OO��������D��E����ʾ������Ϊ�෴��ʱ����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�������ABC�У�����AD��BE����F����ͼ�й��е���������(����)
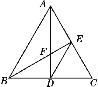
A. 3�� B. 4�� C. 5�� D. 6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ��
��![]() �������
�������![]() ���ס��������ֱ��
���ס��������ֱ��![]() ��
��![]() ����ͬʱ����������ÿСʱ
����ͬʱ����������ÿСʱ![]() ǧ�ף�����ÿСʱ
ǧ�ף�����ÿСʱ![]() ǧ�ף��밴����Ҫ���з��̽��⣺
ǧ�ף��밴����Ҫ���з��̽��⣺
![]() ��ͬʱ������������У�����Сʱ������
��ͬʱ������������У�����Сʱ������
![]() ��ͬʱ������������У��ʱ����������
��ͬʱ������������У��ʱ����������![]() ��
��
![]() ��ͬʱ������ͬ����У��ʱ����������
��ͬʱ������ͬ����У��ʱ����������![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������X��Y�ĶԻ�������и�С�⣺
X���Һ�Y���Ƕ���Σ����������ڽǺ���ӵĽ��Ϊ1440�㣻
Y��X�ı������ҵı���֮��Ϊ1��3.
(1)��X��Y����Ǻ���ӵĶ�����
(2)�ֱ����X��Y�ı�����
(3)�����Y���ж������Խ��ߣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com