
【题目】如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.
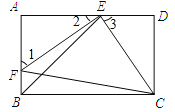
(1)求证:AE=DC;
(2)已知DC=![]() ,求BE的长.
,求BE的长.
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD,AB=6cm,AD=8cm,点O从点B出发,以1cm/s的速度向点C运动,设O点运动时间为t(单位:s)(0<t<4),以点O为圆心,OB为半径作半圆⊙O交BC 于点M,过点A作⊙O的切线交BC于点N,切点为P.

(1)如图2,当点N与点C重合时,求t;
(2)如图3,连接AO,作OQ![]() AO交AN于点Q,连接QM,求证:QM是⊙O的切线;
AO交AN于点Q,连接QM,求证:QM是⊙O的切线;
(3)如图4,连接CP,在点O整个运动过程中,求CP的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C,与x轴交于A,B两点,其中点B的坐标为B(4,0),抛物线的对称轴交x轴于点D,CE∥AB,并与抛物线的对称轴交于点E.现有下列结论:①a>0;②b>0;③4a+2b+c<0;④AD+CE=4.其中所有正确结论的序号是 _____________________ .
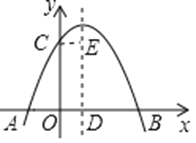
查看答案和解析>>
科目:初中数学 来源: 题型:
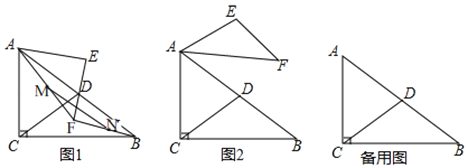
【题目】在Rt△ABC中,∠ACB=90°,AC=BC,CD为AB边上的中线.在Rt△AEF中,∠AEF=90°,AE=EF,AF<AC.连接BF,M,N分别为线段AF,BF的中点,连接MN.
(1)如图1,点F在△ABC内,求证:CD=MN;
(2)如图2,点F在△ABC外,依题意补全图2,连接CN,EN,判断CN与EN的数量关系与位置关系,并加以证明;
(3)将图1中的△AEF绕点A旋转,若AC=a,AF=b(b<a),直接写出EN的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,AM是△ACD的外角∠DAF的平分线.

(1)求证:AM是⊙O的切线;
(2)若∠D = 60°,AD = 2,射线CO与AM交于N点,请写出求ON长的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
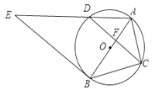
【题目】如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.
(1)若CD=2![]() , AF=3,求⊙O的周长;
, AF=3,求⊙O的周长;
(2)求证:直线BE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(换元思想)阅读材料:
材料1 若一元二次方程![]() 的两根为
的两根为![]() 、
、![]() ,则
,则![]() ,
,![]() .
.
材料2 已知实数![]() 、
、![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
解:由题知![]() 、
、![]() 是方程
是方程![]() 的两个不相等的实数根,根据材料1,得
的两个不相等的实数根,根据材料1,得![]() ,
,![]() .
.
∴![]() .
.
根据上述材料解决下面的问题:
(1)一元二次方程![]() 的两根为
的两根为![]() ,
,![]() ,则
,则![]() ,
,![]() ___________;
___________;
(2)已知实数![]() ,
,![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)已知实数![]() ,
,![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,且点C为⊙O上的一点,∠BAC=30°,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,且∠ECF=∠E.
(1)证明:CF是⊙O的切线;
(2)设⊙O的半径为1,且AC=CE,求MO的长.
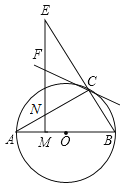
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com