
【题目】如图,AB是⊙O的直径,且点C为⊙O上的一点,∠BAC=30°,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,且∠ECF=∠E.
(1)证明:CF是⊙O的切线;
(2)设⊙O的半径为1,且AC=CE,求MO的长.
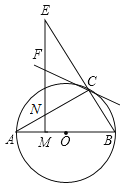
【答案】(1)答案见解析;(2)![]() .
.
【解析】
(1)要证CF为⊙O的切线,只要证明∠OCF=90°即可;
(2)根据三角函数求得AC的长,从而可求得BE的长,再利用三角函数可求出MB的值,从而可得到MO的长.
(1)如图,连接OC.
∵AB是⊙O的直径,∴∠ACB=90°.
∵∠BAC=30°,∴∠ABC=60°;
在Rt△EMB中,∵∠E+∠MBE=90°,∴∠E=30°;
∵∠E=∠ECF,∴∠ECF=30°,∴∠ECF+∠OCB=90°;
∵∠ECF+∠OCB+∠OCF=180°,∴∠OCF=90°,∴CF为⊙O的切线;
(2)在Rt△ACB中,∠A=30°,∠ACB=90°,
∴AC=ABcos30°=![]() ,BC=ABsin30°=1;
,BC=ABsin30°=1;
∵AC=CE,∴BE=BC+CE=1+![]() .
.
在Rt△EMB中,∠E=30°,∠BME=90°,
∴MB=BEsin30°=![]() ,
,
∴MO=MB﹣OB=![]() .
.


科目:初中数学 来源: 题型:
【题目】某市正大力发展绿色农产品,有一种有机水果A特别受欢迎,某超市以市场价格10元/千克在该市收购了6000千克A水果,立即将其冷藏,请根据下列信息解决问题:
①水果A的市场价格每天每千克上涨0.1元;
②平均每天有10千克的该水果损坏,不能出售;
③每天的冷藏费用为300元;
④该水果最多保存110天.
(1)若将这批A水果存放![]() 天后一次性出售,则
天后一次性出售,则![]() 天后这批水果的销售单价为_____元;可以出售的完好水果还有_____千克;
天后这批水果的销售单价为_____元;可以出售的完好水果还有_____千克;
(2)将这批A水果存放多少天后一次性出售所得利润为9600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的图像经过点
的图像经过点![]() ,且它的顶点
,且它的顶点![]() 的横坐标为-1,设抛物线与
的横坐标为-1,设抛物线与![]() 轴交于
轴交于![]() 两点.
两点.
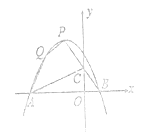
(1)求抛物线的解析式;
(2)求![]() 两点的坐标;
两点的坐标;
(3)设![]() 与
与![]() 轴交于
轴交于![]() 点,连接
点,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小阳在如图所示的扇形舞台上沿O-M-N匀速行走,他从点O出发,沿箭头所示的方向经过点M再走到点N,共用时70秒.有一台摄像机选择了一个固定的位置记录了小阳的走路过程,设小阳走路的时间为t(单位:秒),他与摄像机的距离为y(单位:米),表示y与t的函数关系的图象大致如图②,则这个固定位置可能是图①中的
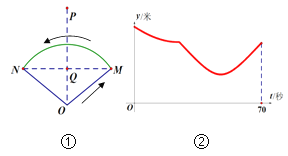
A.点Q B.点P C.点M D.点N
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,在RT△ABC中,∠C=90°,BC=8,AC=6,动点Q从B点开始在线段BA上以每秒2个单位长度的速度向点A移动,同时点P从A点开始在线段AC上以每秒1个单位长度的速度向点C移动.当一点停止运动,另一点也随之停止运动.设点Q,P移动的时间为t秒.当t=____________ 秒时△APQ与△ABC相似.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,![]() 现在有一足够大的直角三角板,它的直角顶点D是BC边上一点,另两条直角边分别交AB、AC于点E、F.
现在有一足够大的直角三角板,它的直角顶点D是BC边上一点,另两条直角边分别交AB、AC于点E、F.

(1)如图1,若DE⊥AB,DF⊥AC,求证:四边形AEDF是矩形
(2)在(1)条件下,若点D在∠BAC的角平分线上,试判断此时四边形AEDF形状,并说明理由;
(3)若点D在∠BAC的角平分线上,将直角三角板绕点D旋转一定的角度,使得直角三角板的两条边与两条直角边分别交于点E、F(如图2),试证明![]() .(尝试作辅助线)
.(尝试作辅助线)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象交x轴于点A,B(点A在点B的左侧).
的图象交x轴于点A,B(点A在点B的左侧).
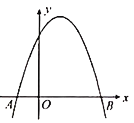
(1)求点A,B的坐标,并根据该函数图象写出y≥0时x的取值范围;
(2)把点B向上平移m个单位得点B1.若点B1向左平移n个单位,将与该二次函数图象上的点B2重合;若点B1向左平移(n+6)个单位,将与该二次函数图象上的点B3重合.已知m>0,n>0,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在等边三角形ABC内,点P到顶点A,B,C的距离分别是3,4,5,则∠APB= ,由于![]() ,PB,PC不在同一三角形中,为了解决本题,我们可以将△ABP绕点A逆时针旋转60o到
,PB,PC不在同一三角形中,为了解决本题,我们可以将△ABP绕点A逆时针旋转60o到![]() 处,连接
处,连接![]() ,此时,
,此时,![]() ≌ ,就可以利用全等的知识,进而将三条线段的长度转化到一个三角形中,从而求出∠APB的度数;
≌ ,就可以利用全等的知识,进而将三条线段的长度转化到一个三角形中,从而求出∠APB的度数;
(2)请你利用第(1)题的解答方法解答:如图②,△ABC中,![]() ,D、E为BC上的点,且
,D、E为BC上的点,且![]() ,求证:
,求证:![]() ;
;
(3)如图③,在△ABC中,![]() ,若以BD、DE、EC为边的三角形是直角三角形时,求BE的长.
,若以BD、DE、EC为边的三角形是直角三角形时,求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com