
【题目】如图,已知抛物线![]() 的图像经过点
的图像经过点![]() ,且它的顶点
,且它的顶点![]() 的横坐标为-1,设抛物线与
的横坐标为-1,设抛物线与![]() 轴交于
轴交于![]() 两点.
两点.
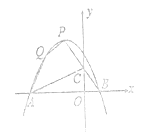
(1)求抛物线的解析式;
(2)求![]() 两点的坐标;
两点的坐标;
(3)设![]() 与
与![]() 轴交于
轴交于![]() 点,连接
点,连接![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ;
;
(2)![]() ,
,![]() ;
;
(3)2.
【解析】
(1)P点的横坐标为-1,那么对称轴![]() ,再把点Q坐标代入即可.
,再把点Q坐标代入即可.
(2)与x轴的交点,此时,函数值y=0,可化为一元二次方程求解.
(3)易求得AB之间的距离,可设出一次函数的解析式,把P、B坐标代入即可求得过P、B的解析式,与y轴的交点就是OC的长.
解:
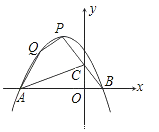
(1)∵P点的横坐标为-1,那么对称轴![]() ,由抛物线
,由抛物线![]() 得,
得,![]() ,
,
并且抛物线经过点![]() ,
,
则有: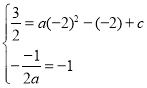
解得:![]() ,
,![]() .
.
∴抛物线解析式为![]()
(2)把y=0代入![]() ,得:
,得:![]() ,
,
整理得![]() .
.
变形为![]() ,
,
解得x1=-3,x2=1.
∵抛物线与x轴的交点A点在x轴负半轴,B点在x轴正半轴,
∴![]() ,
,![]()
(3)将![]() 代入
代入![]() 中得:
中得:![]() ,即
,即![]()
设直线![]() 的解析式为
的解析式为![]()
将![]() ,
,![]() 代入,解得:
代入,解得:![]() ,
,![]()
即直线![]() 的解析式为
的解析式为![]() ,
,
把![]() 代入
代入![]() 中,则
中,则![]()
即![]()
又∵![]()
∴![]()
即![]() 的面积为2
的面积为2


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
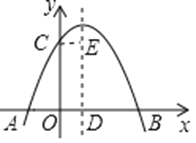
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C,与x轴交于A,B两点,其中点B的坐标为B(4,0),抛物线的对称轴交x轴于点D,CE∥AB,并与抛物线的对称轴交于点E.现有下列结论:①a>0;②b>0;③4a+2b+c<0;④AD+CE=4.其中所有正确结论的序号是 _____________________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(换元思想)阅读材料:
材料1 若一元二次方程![]() 的两根为
的两根为![]() 、
、![]() ,则
,则![]() ,
,![]() .
.
材料2 已知实数![]() 、
、![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
解:由题知![]() 、
、![]() 是方程
是方程![]() 的两个不相等的实数根,根据材料1,得
的两个不相等的实数根,根据材料1,得![]() ,
,![]() .
.
∴![]() .
.
根据上述材料解决下面的问题:
(1)一元二次方程![]() 的两根为
的两根为![]() ,
,![]() ,则
,则![]() ,
,![]() ___________;
___________;
(2)已知实数![]() ,
,![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)已知实数![]() ,
,![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把抛物线y=![]() x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=![]() x2交于点Q,则图中阴影部分的面积为 ▲ .
x2交于点Q,则图中阴影部分的面积为 ▲ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求![]() 的值.
的值.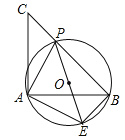
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如果两个正数a,b,即a>0,b>0,有下面的不等式:![]() ,当且仅当a=b时取到等号我们把
,当且仅当a=b时取到等号我们把![]() 叫做正数a,b的算术平均数,把
叫做正数a,b的算术平均数,把![]() 叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最值问题的有力工具.
叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最值问题的有力工具.
初步探究:(1)已知x>0,求函数y=x+![]() 的最小值.
的最小值.
问题迁移:(2)学校准备以围墙一面为斜边,用栅栏围成一个面积为100m2的直角三角形,作为英语角,直角三角形的两直角边各为多少时,所用栅栏最短?
创新应用:(3)如图,在直角坐标系中,直线AB经点P(3,4),与坐标轴正半轴相交于A,B两点,当△AOB的面积最小时,求△AOB的内切圆的半径.
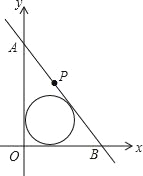
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,且点C为⊙O上的一点,∠BAC=30°,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,且∠ECF=∠E.
(1)证明:CF是⊙O的切线;
(2)设⊙O的半径为1,且AC=CE,求MO的长.
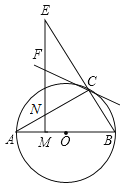
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5G时代即将来临,湖北省提出“建成全国领先、中部一流5G网络”的战略目标.据统计,目前湖北5G基站的数量有1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座.
(1)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率;
(2)若2023年保持前两年5G基站数量的年平均增长率不变,到2023年底,全省5G基站数量能否超过29万座?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
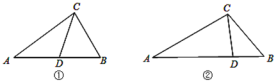
(1)如图①,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD是△ABC的完美分割线;
(2)如图②,在△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com