
【题目】(1)如图①,在等边三角形ABC内,点P到顶点A,B,C的距离分别是3,4,5,则∠APB= ,由于![]() ,PB,PC不在同一三角形中,为了解决本题,我们可以将△ABP绕点A逆时针旋转60o到
,PB,PC不在同一三角形中,为了解决本题,我们可以将△ABP绕点A逆时针旋转60o到![]() 处,连接
处,连接![]() ,此时,
,此时,![]() ≌ ,就可以利用全等的知识,进而将三条线段的长度转化到一个三角形中,从而求出∠APB的度数;
≌ ,就可以利用全等的知识,进而将三条线段的长度转化到一个三角形中,从而求出∠APB的度数;
(2)请你利用第(1)题的解答方法解答:如图②,△ABC中,![]() ,D、E为BC上的点,且
,D、E为BC上的点,且![]() ,求证:
,求证:![]() ;
;
(3)如图③,在△ABC中,![]() ,若以BD、DE、EC为边的三角形是直角三角形时,求BE的长.
,若以BD、DE、EC为边的三角形是直角三角形时,求BE的长.

【答案】(1)150,![]() ;(2)见解析;(3)BE=1+
;(2)见解析;(3)BE=1+![]() 或2+
或2+![]()
【解析】
(1)(1)将△ABP绕顶点A旋转到△AB\P处,△ABP≌△ABP\;进一步说明∠PAP1=60°,再利用等边三角形的判定得出△AP P1为等边三角形,即可得出∠APP'的度数;由勾股定理的逆定理可得∠PP'C=90°,即可得出答案;
(2)把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() .连接
.连接![]() ,
,![]() ;
;
再由"SAS"得到![]() ,可得DE=DG,即可把EF,BE,FC放到一个直角三角形中,用勾股定理证明即可;
,可得DE=DG,即可把EF,BE,FC放到一个直角三角形中,用勾股定理证明即可;
(3)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,可得
,可得![]() ,然后根据全等三角形的性质和已知条件说明
,然后根据全等三角形的性质和已知条件说明![]() ,可得DF=DE,由以BD、DE、EC为边的三角形是直角三角形,分情况讨论,由直角三角形的性质可求解即可.
,可得DF=DE,由以BD、DE、EC为边的三角形是直角三角形,分情况讨论,由直角三角形的性质可求解即可.
(1)解:(1)将△ABP绕顶点A旋转到△AB\P处,
∴△ABP≌△ABP\
∴AB=AC,AP=AP\,∠BAP=∠CAP\
∴∠BAC=∠PAP\=60°
∴△APP\是等边三角形
∴∠APP\=600
∵P\C=PB=4,PP'=PA=3,PC=5,
∴PC2=25=P\P2+P\C2=9+16
∴∠PP\C=90°
∴APP\C是直角三角形,
∴∠APB=∠AP\C=∠APP\∠LP\PC=60°+90°=150°
故答案为:150,△ABP
150,![]()
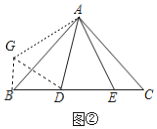
(2)如图2,把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() .连接
.连接![]() ,
,
则![]() .
.
![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() .
.
![]() ,
,
在![]() 和
和![]() 中,
中,
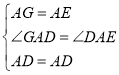 ,
,
![]() .
.
![]() ,
,
又![]() ,
,
![]() ,即
,即![]() ;
;
(3)如图3,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,,
,,
![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,且
,且![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() 以
以![]() 、
、![]() 、
、![]() 为边的三角形是直角三角形,
为边的三角形是直角三角形,
![]() 以
以![]() 、
、![]() 、
、![]() 为边的三角形是直角三角形,
为边的三角形是直角三角形,![]() 是直角三角形,
是直角三角形,
若![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
若![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]()
![]()
∴ 综上所述,BE=1+![]() 或2+
或2+![]()


 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,且点C为⊙O上的一点,∠BAC=30°,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,且∠ECF=∠E.
(1)证明:CF是⊙O的切线;
(2)设⊙O的半径为1,且AC=CE,求MO的长.
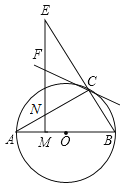
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△BEC均为等腰直角三角形,且∠ACB=∠BEC=90°,点P为线段BE延长线上一点,连接CP,以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F.
(1)求证:![]() ;
;
(2)连接BD,请你判断AC与BD有什么位置关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
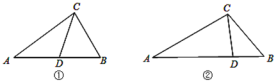
(1)如图①,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD是△ABC的完美分割线;
(2)如图②,在△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
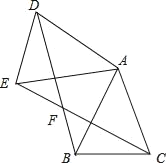
(1)求证:△AEC≌△ADB;(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙P的直径,点![]() 在⊙P上,
在⊙P上,![]() 为⊙P外一点,且∠ADC=90°,直线
为⊙P外一点,且∠ADC=90°,直线![]() 为⊙P的切线.
为⊙P的切线.
⑴ 试说明:2∠B+∠DAB=180°
⑵ 若∠B=30°,AD=2,求⊙P的半径.
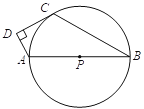
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中, A(0,2),B(-1,0),Rt△AOC的面积为4.
(1)求点C的坐标;
(2)抛物线![]() 经过A、B、C三点,求抛物线的解析式和对称轴;
经过A、B、C三点,求抛物线的解析式和对称轴;
(3)设点P(m,n)是抛物线在第一象限部分上的点,△PAC的面积为S,求S关于m的函数关系式,并求使S最大时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班部分学生接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了如图①②两幅不完整的统计图,请根据图中的信息解答下列问题.
(1)九年级(1)班接受调查的学生共有多少名?
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系式和自变量![]() 的取值范围;
的取值范围;
(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com