
ЁОЬтФПЁПФГЪае§ДѓСІЗЂеЙТЬЩЋХЉВњЦЗЃЌгавЛжжгаЛњЫЎЙћAЬиБ№ЪмЛЖгЃЌФГГЌЪавдЪаГЁМлИё10дЊ/ЧЇПЫдкИУЪаЪеЙКСЫ6000ЧЇПЫAЫЎЙћЃЌСЂМДНЋЦфРфВиЃЌЧыИљОнЯТСааХЯЂНтОіЮЪЬтЃК
ЂйЫЎЙћAЕФЪаГЁМлИёУПЬьУПЧЇПЫЩЯеЧ0.1дЊЃЛ
ЂкЦНОљУПЬьга10ЧЇПЫЕФИУЫЎЙћЫ№ЛЕЃЌВЛФмГіЪлЃЛ
ЂлУПЬьЕФРфВиЗбгУЮЊ300дЊЃЛ
ЂмИУЫЎЙћзюЖрБЃДц110ЬьЃЎ
(1)ШєНЋетХњAЫЎЙћДцЗХ![]() ЬьКѓвЛДЮадГіЪлЃЌдђ
ЬьКѓвЛДЮадГіЪлЃЌдђ![]() ЬьКѓетХњЫЎЙћЕФЯњЪлЕЅМлЮЊ_____дЊЃЛПЩвдГіЪлЕФЭъКУЫЎЙћЛЙга_____ЧЇПЫЃЛ
ЬьКѓетХњЫЎЙћЕФЯњЪлЕЅМлЮЊ_____дЊЃЛПЩвдГіЪлЕФЭъКУЫЎЙћЛЙга_____ЧЇПЫЃЛ
(2)НЋетХњAЫЎЙћДцЗХЖрЩйЬьКѓвЛДЮадГіЪлЫљЕУРћШѓЮЊ9600дЊЃП
ЁОД№АИЁП(1)![]() ЃЛ
ЃЛ![]() ЃЛ(2)етХњAЫЎЙћДцЗХ80ЗђКѓвЛДЮадГіЪлЫљЕУРћШѓЮЊ9600дЊЃЎ
ЃЛ(2)етХњAЫЎЙћДцЗХ80ЗђКѓвЛДЮадГіЪлЫљЕУРћШѓЮЊ9600дЊЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЯњЪлМл=ГЩБОМл+УПЬьУПЧЇПЫЩЯеЧ0.1дЊЬюПеЃЛЭъКУЫЎЙћЕФжЪСП=змжЪСП-Ы№ЛЕЕФЫЎЙћЕФжЪСПЃЛ
ЃЈ2ЃЉАДееЕШСПЙиЯЕЁАРћШѓ=ЯњЪлзмН№Жю-ЪеЙКГЩБО-ИїжжЗбгУЁБСаГіЗНГЬЧѓНтМДПЩЃЎ
(1) 10+0.1xЃЛ6000-10xЃЎ
ЙЪД№АИЪЧЃК10+0.1xЃЛ6000-10xЃЛ
(2)ЩшДцЗХ![]() ЬьКѓвЛДЮадГіЪлЫљЕУРћШѓЮЊ9600дЊЃЌ
ЬьКѓвЛДЮадГіЪлЫљЕУРћШѓЮЊ9600дЊЃЌ
ИљОнЬтвтЕУЃЌ![]() ЃЌ
ЃЌ
НтЕУ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
Ёп![]() ЃЌ
ЃЌ
ЁретХњAЫЎЙћДцЗХ80ЬьКѓвЛДЮадГіЪлЫљЕУРћШѓЮЊ9600дЊЃЎ


 ЬвРюЮФЛЏПьРжЪюМйЮфККГіАцЩчЯЕСаД№АИ
ЬвРюЮФЛЏПьРжЪюМйЮфККГіАцЩчЯЕСаД№АИ гХауЩњПьРжМйЦкУПвЛЬьШЋаТКЎМйзївЕБОЯЕСаД№АИ
гХауЩњПьРжМйЦкУПвЛЬьШЋаТКЎМйзївЕБОЯЕСаД№АИ ЪюМйНгСІШќаТНЎЧрЩйФъГіАцЩчЯЕСаД№АИ
ЪюМйНгСІШќаТНЎЧрЩйФъГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌОиаЮABCDЃЌAB=6cmЃЌAD=8cmЃЌЕуOДгЕуBГіЗЂЃЌвд1cm/sЕФЫйЖШЯђЕуCдЫЖЏЃЌЩшOЕудЫЖЏЪБМфЮЊtЃЈЕЅЮЛЃКsЃЉЃЈ0<t<4ЃЉЃЌвдЕуOЮЊдВаФЃЌOBЮЊАыОЖзїАыдВЁбOНЛBC гкЕуMЃЌЙ§ЕуAзїЁбOЕФЧаЯпНЛBCгкЕуNЃЌЧаЕуЮЊP.

ЃЈ1ЃЉШчЭМ2ЃЌЕБЕуNгыЕуCжиКЯЪБЃЌЧѓtЃЛ
ЃЈ2ЃЉШчЭМ3ЃЌСЌНгAOЃЌзїOQ![]() AOНЛANгкЕуQЃЌСЌНгQMЃЌЧѓжЄЃКQMЪЧЁбOЕФЧаЯпЃЛ
AOНЛANгкЕуQЃЌСЌНгQMЃЌЧѓжЄЃКQMЪЧЁбOЕФЧаЯпЃЛ
ЃЈ3ЃЉШчЭМ4ЃЌСЌНгCPЃЌдкЕуOећИідЫЖЏЙ§ГЬжаЃЌЧѓCPЕФзюаЁжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
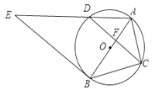
ЁОЬтФПЁПШчЭМЃЌЁбOЪЧЁїABCЕФЭтНгдВЃЌABОЙ§ЕуOЃЌCDЪЧЯвЃЌЧвCDЁЭABгкЕуFЃЌСЌНгADЃЌЙ§ЕуBЕФжБЯпгыЯпЖЮADЕФбгГЄЯпНЛгкЕуEЃЌЧвЁЯE=ЁЯACFЃЎ
ЃЈ1ЃЉШєCD=2![]() ЃЌ AF=3ЃЌЧѓЁбOЕФжмГЄЃЛ
ЃЌ AF=3ЃЌЧѓЁбOЕФжмГЄЃЛ
ЃЈ2ЃЉЧѓжЄЃКжБЯпBEЪЧЁбOЕФЧаЯпЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЛЛдЊЫМЯыЃЉдФЖСВФСЯЃК
ВФСЯ1 ШєвЛдЊЖўДЮЗНГЬ![]() ЕФСНИљЮЊ
ЕФСНИљЮЊ![]() ЁЂ
ЁЂ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() .
.
ВФСЯ2 вбжЊЪЕЪ§![]() ЁЂ
ЁЂ![]() Тњзу
Тњзу![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
НтЃКгЩЬтжЊ![]() ЁЂ
ЁЂ![]() ЪЧЗНГЬ
ЪЧЗНГЬ![]() ЕФСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌИљОнВФСЯ1ЃЌЕУ
ЕФСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌИљОнВФСЯ1ЃЌЕУ![]() ЃЌ
ЃЌ![]() .
.
Ёр![]() .
.
ИљОнЩЯЪіВФСЯНтОіЯТУцЕФЮЪЬтЃК
ЃЈ1ЃЉвЛдЊЖўДЮЗНГЬ![]() ЕФСНИљЮЊ
ЕФСНИљЮЊ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() ___________ЃЛ
___________ЃЛ
ЃЈ2ЃЉвбжЊЪЕЪ§![]() ЃЌ
ЃЌ![]() Тњзу
Тњзу![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉвбжЊЪЕЪ§![]() ЃЌ
ЃЌ![]() Тњзу
Тњзу![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
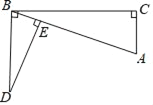
ЁОЬтФПЁПШчЭМЃЌЁЯC=ЁЯCBD=90ЁуЃЌDEЁЭABгкЕуEЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїDBEЁзЁїBACЃЎ
ЃЈ2ЃЉШєBC=3ЃЌDB=2ЃЌCA=1ЃЌЧѓDEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАбХзЮяЯпy=![]() x2ЦНвЦЕУЕНХзЮяЯпmЃЌХзЮяЯпmОЙ§ЕуAЃЈЉ6ЃЌ0ЃЉКЭдЕуOЃЈ0ЃЌ0ЃЉЃЌЫќЕФЖЅЕуЮЊPЃЌЫќЕФЖдГЦжсгыХзЮяЯпy=
x2ЦНвЦЕУЕНХзЮяЯпmЃЌХзЮяЯпmОЙ§ЕуAЃЈЉ6ЃЌ0ЃЉКЭдЕуOЃЈ0ЃЌ0ЃЉЃЌЫќЕФЖЅЕуЮЊPЃЌЫќЕФЖдГЦжсгыХзЮяЯпy=![]() x2НЛгкЕуQЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊЁЁ Ёј ЁЁЃЎ
x2НЛгкЕуQЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊЁЁ Ёј ЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕШбќжБНЧШ§НЧаЮABCЃЌЕуPЪЧаББпBCЩЯвЛЕуЃЈВЛгыBЃЌCжиКЯЃЉЃЌPEЪЧЁїABPЕФЭтНгдВЁбOЕФжБОЖЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїAPEЪЧЕШбќжБНЧШ§НЧаЮЃЛ
ЃЈ2ЃЉШєЁбOЕФжБОЖЮЊ2ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ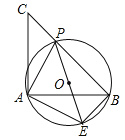
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЧвЕуCЮЊЁбOЩЯЕФвЛЕуЃЌЁЯBAC=30ЁуЃЌMЪЧOAЩЯвЛЕуЃЌЙ§MзїABЕФДЙЯпНЛACгкЕуNЃЌНЛBCЕФбгГЄЯпгкЕуEЃЌжБЯпCFНЛENгкЕуFЃЌЧвЁЯECF=ЁЯEЃЎ
ЃЈ1ЃЉжЄУїЃКCFЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЩшЁбOЕФАыОЖЮЊ1ЃЌЧвAC=CEЃЌЧѓMOЕФГЄЃЎ
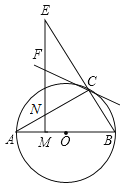
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCКЭЁїBECОљЮЊЕШбќжБНЧШ§НЧаЮЃЌЧвЁЯACB=ЁЯBEC=90ЁуЃЌЕуPЮЊЯпЖЮBEбгГЄЯпЩЯвЛЕуЃЌСЌНгCPЃЌвдCPЮЊжБНЧБпЯђЯТзїЕШбќжБНЧЁїCPDЃЌЯпЖЮBEгыCDЯрНЛгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉСЌНгBDЃЌЧыФуХаЖЯACгыBDгаЪВУДЮЛжУЙиЯЕЃПВЂЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com