
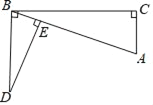
【题目】如图,∠C=∠CBD=90°,DE⊥AB于点E.
(1)求证:△DBE∽△BAC.
(2)若BC=3,DB=2,CA=1,求DE的长.
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.下面有三个推断:①某次实验投掷次数是500,计算机记录“钉尖向上”的次数是308,则该次试验“钉尖向上”的频率是0.616;②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.其中合理的是( )

A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2ax+c交x轴于A,B两点,交y轴于点C(0,3),tan∠OAC=![]() .
.
(1)求抛物线的解析式;
(2)点H是线段AC上任意一点,过H作直线HN⊥x轴于点N,交抛物线于点P,求线段PH的最大值;
(3)点M是抛物线上任意一点,连接CM,以CM为边作正方形CMEF,是否存在点M使点E恰好落在对称轴上?若存在,请求出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的材料,然后解答问题.通过计算,发现方程:
![]() 的解为
的解为![]() ,
,![]() ;
;
![]() 的解为
的解为![]() ,
,![]() ;
;
![]() 的解为
的解为![]() ,
,![]() ;
;
……
(1)观察上述方程的解,猜想关于![]() 的方程
的方程![]() 的解是_____.
的解是_____.
(2)根据上面的规律,猜想关于![]() 的方程
的方程![]() 的解是_______.
的解是_______.
(3)类似地,关于![]() 的方程
的方程![]() 的解是______.
的解是______.
(4)请利用上述规律求关于![]() 的方程
的方程![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
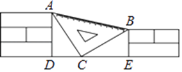
【题目】课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间(如图),已知,∠ACB=90°,AC=BC, AB=26.如果每块砖的厚度相等,砖缝厚度忽略不计,那么砌墙砖块的厚度为( )
A.![]() B.
B.![]() C.
C.![]() D.5
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2m+1)x+m2+![]() =0有两个不相等的实数根.
=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为(1)中符合条件的最小正整数,设此时对应的一元二次方程的两个实数根分别为α,β,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】善于学习的小明在学习了一次方程(组),一元一次不等式和一次函数后,把相关知识归纳整理如下:

(1)请你根据以上方框中的内容在下面数字序号后写出相应的结论:
① ;② ;③ ;④ ;
(2)如果点C的坐标为(1,3),那么不等式kx+b≤k1x+b1的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
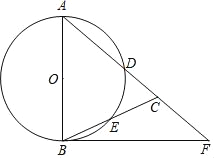
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交AC、BC于点D、E,点F在AC的延长线上,且∠A=2∠CBF.
(1)求证:BF与⊙O相切.
(2)若BC=CF=4,求BF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com