
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2ax+c交x轴于A,B两点,交y轴于点C(0,3),tan∠OAC=![]() .
.
(1)求抛物线的解析式;
(2)点H是线段AC上任意一点,过H作直线HN⊥x轴于点N,交抛物线于点P,求线段PH的最大值;
(3)点M是抛物线上任意一点,连接CM,以CM为边作正方形CMEF,是否存在点M使点E恰好落在对称轴上?若存在,请求出点M的坐标;若不存在,请说明理由.

【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+3;(2)
x+3;(2)![]() ;(3)点M的坐标是(﹣4,0),(﹣
;(3)点M的坐标是(﹣4,0),(﹣![]() ,
,![]() ),(﹣
),(﹣![]() ,
,![]() )或(2,0).
)或(2,0).
【解析】
试题(1)由点C的坐标以及tan∠OAC=![]() 可得出点A的坐标,结合点A、C的坐标利用待定系数法即可求出抛物线的解析式;(2)设直线AC的解析式为y=kx+b,由点A、C的解析式利用待定系数法即可求出直线AC的解析式,设N(x,0)(﹣4<x<0),可找出H、P的坐标,由此即可得出PH关于x的解析式,利用配方法即二次函数的性质即可解决最值问题;(3)过点M作MK⊥y轴于点K,交对称轴于点G,根据角的计算依据正方形的性质即可得出△MCK≌△MEG(AAS),进而得出MG=CK.设出点M的坐标利用正方形的性质即可得出点G、K的坐标,由正方形的性质即可得出关于x的含绝对值符号的一元二次方程,解方程即可求出x值,将其代入抛物线解析式中即可求出点M的坐标.
可得出点A的坐标,结合点A、C的坐标利用待定系数法即可求出抛物线的解析式;(2)设直线AC的解析式为y=kx+b,由点A、C的解析式利用待定系数法即可求出直线AC的解析式,设N(x,0)(﹣4<x<0),可找出H、P的坐标,由此即可得出PH关于x的解析式,利用配方法即二次函数的性质即可解决最值问题;(3)过点M作MK⊥y轴于点K,交对称轴于点G,根据角的计算依据正方形的性质即可得出△MCK≌△MEG(AAS),进而得出MG=CK.设出点M的坐标利用正方形的性质即可得出点G、K的坐标,由正方形的性质即可得出关于x的含绝对值符号的一元二次方程,解方程即可求出x值,将其代入抛物线解析式中即可求出点M的坐标.
试题解析:(1)∵C(0,3),
∴OC=3,
∵tan∠OAC=![]() ,
,
∴OA=4,
∴A(﹣4,0).
把A(﹣4,0)、C(0,3)代入y=ax2+2ax+c中,
得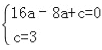 ,解得:
,解得: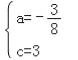 ,
,
∴抛物线的解析式为y=﹣![]() x2﹣
x2﹣![]() x+3.
x+3.
(2)设直线AC的解析式为y=kx+b,
把A(﹣4,0)、C(0,3)代入y=kx+b中,
得:![]() ,解得:
,解得: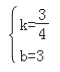 ,
,
∴直线AC的解析式为y=![]() x+3.
x+3.
设N(x,0)(﹣4<x<0),则H(x,![]() x+3),P(x,﹣
x+3),P(x,﹣![]() x2﹣
x2﹣![]() x+3),
x+3),
∴PH=﹣![]() x2﹣
x2﹣![]() x+3﹣(
x+3﹣(![]() x+3)=﹣
x+3)=﹣![]() x2﹣
x2﹣![]() x=﹣
x=﹣![]() (x﹣2)2+
(x﹣2)2+![]() ,
,
∵﹣![]() <0,
<0,
∴PH有最大值,
当x=2时,PH取最大值,最大值为![]() .
.
(3)过点M作MK⊥y轴于点K,交对称轴于点G,则∠MGE=∠MKC=90°,
∴∠MEG+∠EMG=90°,
∵四边形CMEF是正方形,
∴EM=MC,∠MEC=90°,
∴∠EMG+∠CMK=90°,
∴∠MEG=∠CMK.
在△MCK和△MEG中,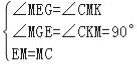 ,
,
∴△MCK≌△MEG(AAS),
∴MG=CK.
由抛物线的对称轴为x=﹣1,设M(x,﹣![]() x2﹣
x2﹣![]() x+3),则G(﹣1,﹣
x+3),则G(﹣1,﹣![]() x2﹣
x2﹣![]() x+3),K(0,﹣
x+3),K(0,﹣![]() x2﹣
x2﹣![]() x+3),
x+3),
∴MG=|x+1|,CK=|﹣![]() x2﹣
x2﹣![]() x+3﹣3|=|﹣
x+3﹣3|=|﹣![]() x2﹣
x2﹣![]() x|=|
x|=|![]() x2+
x2+![]() x|,
x|,
∴|x+1|=|![]() x2+
x2+![]() x|,
x|,
∴![]() x2+
x2+![]() x=±(x+1),
x=±(x+1),
解得:x1=﹣4,x2=﹣![]() ,x3=﹣
,x3=﹣![]() ,x4=2,
,x4=2,
代入抛物线解析式得:y1=0,y2=![]() ,y3=
,y3=![]() ,y4=0,
,y4=0,
∴点M的坐标是(﹣4,0),(﹣![]() ,
,![]() ),(﹣
),(﹣![]() ,
,![]() )或(2,0).
)或(2,0).


科目:初中数学 来源: 题型:
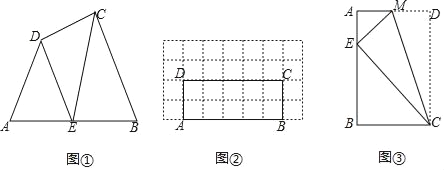
【题目】在四边形ABCD中,∠B=∠C=90°,AB=3,BC=4,CD=1.以AD为腰作等腰△ADE,使∠ADE=90°,过点E作EF⊥DC交直线CD于点F.请画出图形,并直接写出AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料阅读:
如图①,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.
解决问题:
(1)图①中,若∠A=∠B=∠DEC=40°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图②,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点(无需写解答过程);
(3)如图③所示的矩形ABCD,将矩形ABCD沿CM折叠后,点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究点E的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
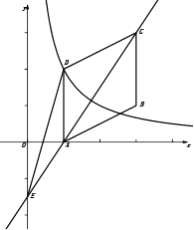
【题目】(本题满分10分)如图,在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),双曲线y=![]() (k≠0,x>0)过点D.
(k≠0,x>0)过点D.
(1)求此双曲线的解析式;
(2)作直线AC交y轴于点E,连结DE,求△ CDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)读读做做:教材中有这样的问题,观察下面的式子,探索它们的规律,![]() =1-
=1-![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ……用正整数n表示这个规律是______;
……用正整数n表示这个规律是______;
(2)问题解决:一容器装有1L水,按照如下要求把水倒出:第一次倒出![]() L水,第二次倒出的水量是
L水,第二次倒出的水量是![]() L水的
L水的![]() ,第三次倒出的水量是
,第三次倒出的水量是![]() L水的
L水的![]() ,第四次倒出的水量是
,第四次倒出的水量是![]() L水的
L水的![]() ,……,第n+1次倒出的水量是
,……,第n+1次倒出的水量是![]() L水的
L水的![]() ,……,按照这种倒水方式,这1L水能否倒完?
,……,按照这种倒水方式,这1L水能否倒完?
(3)拓展探究:①解方程:![]() +
+![]() +
+![]() +
+![]() =
=![]() ;
;
②化简:![]() +
+![]() +
+![]() …+
…+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑经销商计划购进一批电脑机箱和液晶显示器,若购电脑机箱10台和液液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点.
(1)如图,E、F分别是AB、AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
(2)若E、F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?画出图形,写出结论不证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com