
【题目】在四边形ABCD中,∠B=∠C=90°,AB=3,BC=4,CD=1.以AD为腰作等腰△ADE,使∠ADE=90°,过点E作EF⊥DC交直线CD于点F.请画出图形,并直接写出AF的长.
【答案】2![]() 或2
或2![]()
【解析】
如图,分两种情况讨论,E点可在AD的上方,由已知条件可证的△ADM≌△EDF,可得DF=DM,后可求得FN的长,可求得AF的长;
E点可在AD的下方,同理可证△ADN≌△DEF,可得DF=DM,可求得FN的长后的AF的长.
如图1中,作AN⊥CF于N,DM⊥AB于M.
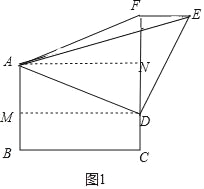
∵∠B=∠C=∠DMB=90°,
∴四边形BCDM是矩形,易证四边形AMDN是矩形,
∴CD=BM=1,AM=AB﹣BM=2,DM=BC=AN=4,DN=AM=2,
∵∠AMD=∠DFE,∠ADM=∠FDE,DA=DE,
∴△ADM≌△EDF,
∴DF=DM=4,
∴FN=DF﹣DN=2,
在Rt△AFN中,AF=![]() =2
=2![]() .
.
如图2中,作AN⊥FD交FD的延长线于N.
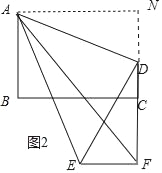
易证AN=BC=4,△ADN≌△DEF,
∴DF=AN=4,DN=CN﹣CD=2,
∴FN=6,
在Rt△AFN中,AF=![]() =2
=2![]() .
.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】在甲村至乙村的公路旁有一块山地正在开发,现有一![]() 处需要爆破.已知点
处需要爆破.已知点![]() 与公路上的停靠站
与公路上的停靠站![]() 的距离为
的距离为![]() 米,与公路上另一停靠站
米,与公路上另一停靠站![]() 的距离为
的距离为![]() 米,且
米,且![]() ,如图,为了安全起见,爆破点
,如图,为了安全起见,爆破点![]() 周围半径
周围半径![]() 米范围内不得进入,问在进行爆破时,公路
米范围内不得进入,问在进行爆破时,公路![]() 段是否有危险,是否需要暂时封锁?请通过计算进行说明.
段是否有危险,是否需要暂时封锁?请通过计算进行说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
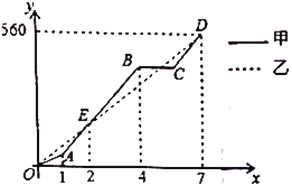
【题目】端午节期间,甲、乙两人沿同一路线行驶,各自开车同时去离家![]() 千米的景区游玩,甲先以每小时
千米的景区游玩,甲先以每小时![]() 千米的速度匀速行驶
千米的速度匀速行驶![]() 小时,再以每小时
小时,再以每小时![]() 千米的速度匀速行驶,途中休息了一段时间后,仍按照每小时
千米的速度匀速行驶,途中休息了一段时间后,仍按照每小时![]() 千米的速度匀速行驶,两人同时到达目的地,图中折线、线段分别表示甲、乙两人所走的路程
千米的速度匀速行驶,两人同时到达目的地,图中折线、线段分别表示甲、乙两人所走的路程![]() 、
、![]() 与时间
与时间![]() 之间的函数关系的图象请根据图象提供的信息,解决下列问题:
之间的函数关系的图象请根据图象提供的信息,解决下列问题:
(1)乙的速度为:_______;
(2)图中![]() 点的坐标是________;
点的坐标是________;
(3)图中![]() 点的坐标是________;
点的坐标是________;
(4)题中![]() _________;
_________;
(5)甲在途中休息____________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD和矩形PEFG中,AB=8,BC=6,PE=2,PG=4.PE与AC交于点M,EF与AC交于点N,动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,伴随点P的运动,矩形PEFG在射线AB上滑动;动点K从点P出发沿折线PE﹣﹣EF以每秒1个单位长的速度匀速运动.点P、K同时开始运动,当点K到达点F时停止运动,点P也随之停止.设点P、K运动的时间是t秒(t>0).
(1)当t=1时,KE=_____,EN=_____;
(2)当t为何值时,△APM的面积与△MNE的面积相等?
(3)当点K到达点N时,求出t的值;
(4)当t为何值时,△PKB是直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
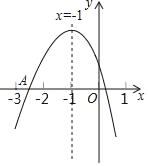
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,下列结论中:
①abc<0;②9a﹣3b+c<0;③b2﹣4ac>0;④a>b,
正确的结论是_____(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,点F是射线DC上一动点(不与C,D重合).连接AF并延长交直线BC于点E,交BD于H,连接CH,过点C作CG⊥HC交AE于点G.
(1)若点F在边CD上,如图1.
①证明:∠DAH=∠DCH;
②猜想:△GFC的形状并说明理由.
(2)取DF中点M,连接MG.若MG=2.5,正方形边长为4,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店现有资金7700元,计划全部用于购进甲、乙、丙三种图书共20套,其中甲种图书每套500元,乙种图书每套400元,丙种图书每套250元.书店将甲、乙、丙三种图书的售价分别定为每套550元,430元,310元.设书店购进甲种图书x套,乙种图书y套,请解答下列问题:
(1)请求出y与x的函数关系式(不需要写出自变量的取值范围);
(2)若书店购进甲、乙两种图书均不少于1套,则该书店有几种进货方案?
(3)在(1)和(2)的条件下,根据市场调查,书店决定将三种图书的售价作如下调整:甲种图书的售价不变,乙种图书的售价上调a(a为正整数)元,丙种图书的售价下调a元,这样三种图书全部售出后,所获得的利润比(2)中某方案的利润多出20元,请直接写出书店是按哪种方案进的货及a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.下面有三个推断:①某次实验投掷次数是500,计算机记录“钉尖向上”的次数是308,则该次试验“钉尖向上”的频率是0.616;②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.其中合理的是( )

A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2ax+c交x轴于A,B两点,交y轴于点C(0,3),tan∠OAC=![]() .
.
(1)求抛物线的解析式;
(2)点H是线段AC上任意一点,过H作直线HN⊥x轴于点N,交抛物线于点P,求线段PH的最大值;
(3)点M是抛物线上任意一点,连接CM,以CM为边作正方形CMEF,是否存在点M使点E恰好落在对称轴上?若存在,请求出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com