
【题目】已知正方形ABCD,点F是射线DC上一动点(不与C,D重合).连接AF并延长交直线BC于点E,交BD于H,连接CH,过点C作CG⊥HC交AE于点G.
(1)若点F在边CD上,如图1.
①证明:∠DAH=∠DCH;
②猜想:△GFC的形状并说明理由.
(2)取DF中点M,连接MG.若MG=2.5,正方形边长为4,求BE的长.

【答案】(1)①证明见解析;②△GFC是等腰三角形,理由见解析;(2)BE的长为1或7.
【解析】
(1)①根据正方形的性质可得AD=CD,∠ADH=∠CDH,利用SAS可证明△ADH≌△CDH,即可得∠DAH=∠DCH;
②由正方形的性质可得∠DAH+∠AFD=90°,由CG⊥HC可得∠DCH+∠FCG=90°,根据∠AFD=∠CFG,可得∠CFG=∠FCG,即可证明CG=FG,可得△GFC是等腰三角形;
(2)当点F在线段CD上时,连接DE,根据正方形的性质及角的和差关系可得∠E=∠GCE,即可证明CG=EG,由△GFC是等腰三角形可得CG=GF,可得点G为EF中点,即可证明GM是△FDE的中位线,根据中位线的性质可求出DE的长,利用勾股定理可求出CE的长,进而根据BE=BC+CE即可求出BE的长;当点F在DC延长线上时,连接DE,同理可得MG为△FDE的中位线,可求出DE的长,利用勾股定理可求出CE的长,根据BE=BC-CE即可求出BE的长.
(1)①∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ADB=∠CDB=45°,
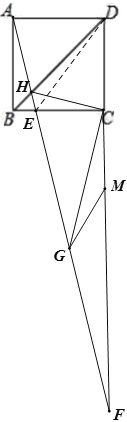
在△ADH和△CDH中,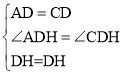 ,
,
∴△ADH≌△CDH,
∴∠DAH=∠DCH.
②△GFC是等腰三角形,理由如下:
∵四边形ABCD是正方形,CG⊥HC,
∴∠ADF=∠HCG=90°,
∴∠DAH+∠AFD=DCH+∠DCG=90°,
∵∠DAH=∠DCH,∠HFD=∠CFG,
∴∠CFG=∠GCF,
∴CF=CG,
∴△GFC是等腰三角形.
(2)如图,当点F在线段CD上时,连接DE,
∵四边形ABCD是正方形,
∴∠CEF+∠CFG=90°,∠GCE+∠GCF=90°,
∵∠CFG=∠GCF,
∴∠CEF=∠GCE,
∴CG=EG,
∵CG=FG,
∴FG=EG,
∵点M是DF的中点,
∴GM是△DFE的中位线,
∵GM=2.5,
∴DE=2GM=5,
∵正方形ABCD的边长为4,
∴CE=![]() =3,
=3,
∴BE=BC+CE=4+3=7.
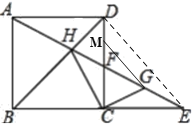
如图,当点F在DC的延长线上时,连接DE,
同理可得:MG为△DFE的中位线,
∴DE=2GM=5,
∴CE=![]() =3,
=3,
∴BE=BC-CE=4-3=1,
综上所述:BE的长为1或7.


 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
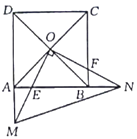
【题目】如图,正方形![]() 的对角线交于点
的对角线交于点![]() 点
点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上(
上(![]() )且
)且![]() ,
,![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,
,![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.
(1)求证:![]() .
.
(2)若正方形![]() 的边长为4,
的边长为4,![]() 为
为![]() 的中点,求
的中点,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一列有理数﹣1,2,﹣3,4,﹣5,6,……,如图所示有序排列.根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰6”中C的位置是有理数_____,2018应排在A,B,C,D,E中的_____位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△BAD≌△EBC,∠BAD=∠BCE=90°,∠ABD=∠BEC=30°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)如图1,当A,B,E三点在同一直线上时,判断AC与CN数量关系为________;
(2)将图1中△BCE绕点B逆时针旋转到图2位置时,(1)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由;
(3)将图1中△BCE绕点B逆时针旋转一周,旋转过程中△CAN能否为等腰直角三角形?若能,直接写出旋转角度;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在直角坐标系xOy中,点A,点B坐标分别为(﹣1,0),(0, ![]() ),连结AB,OD由△AOB绕O点顺时针旋转60°而得.
),连结AB,OD由△AOB绕O点顺时针旋转60°而得.
(1)求点C的坐标;
(2)△AOB绕点O顺时针旋转60°所扫过的面积;
(3)线段AB绕点O顺时针旋转60°所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如 图,在边长为3 cm的正方形ABCD中,点E为BC边上的任意一点,AF⊥AE,AF交CD的延长线于F,则四边形AFCE的面积为_____cm2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com