【题目】将一列有理数﹣1，2，﹣3，4，﹣5，6，……，如图所示有序排列．根据图中的排列规律可知，“峰1”中峰顶的位置（C的位置）是有理数4，那么，“峰6”中C的位置是有理数_____，2018应排在A，B，C，D，E中的_____位置．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），……，按这样的运动规律，经过第2019次运动后，动点P的坐标是（ ）
A. （2018，1）B. （2018,0）C. （2019,2） D. （2019,1）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ACB=90°，∠A=40°，△ABC的外角∠CBD的平分线BE交AC的延长线于点E．
（1）求∠CBE的度数；
（2）过点D作DF∥BE，交AC的延长线于点F，求∠F的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为传播“绿色出行，低碳生活”的理念，小贾同学的爸爸从家里出发，骑自行车去图书馆看书，图1表达的是小贾的爸爸行驶的路程
（米）与行驶时间
（分钟）的变化关系
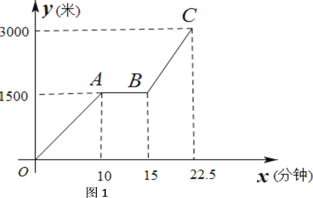
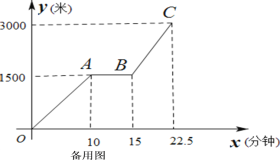
（1）求线段BC所表达的函数关系式；
（2）如果小贾与爸爸同时从家里出发，小贾始终以速度120米/分钟行驶，当小贾与爸爸相距100米是，求小贾的行驶时间；
（3）如果小贾的行驶速度是
米/分，且在途中与爸爸恰好相遇两次（不包括家、图书馆两地），请直接写出的取值范围。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若数a使关于x的不等式组
，有且仅有四个整数解，且使关于y的分式方程
有非负数解，则所有满足条件的整数a的值之和是________________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知正方形ABCD，点F是射线DC上一动点(不与C，D重合)．连接AF并延长交直线BC于点E，交BD于H，连接CH，过点C作CG⊥HC交AE于点G．
（1）若点F在边CD上，如图1．
①证明：∠DAH=∠DCH；
②猜想：△GFC的形状并说明理由．
（2）取DF中点M，连接MG．若MG=2.5，正方形边长为4，求BE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：我们把对角线互相垂直的四边形叫做垂美四边形．
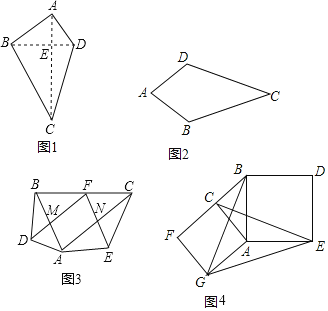
（1）概念理解：如图2，在四边形ABCD中，AB=AD，CB=CD，那么四边形ABCD是垂美四边形吗？请说明理由．
（2）性质探究：
①如图1，垂美四边形ABCD两组对边AB、CD与BC、AD之间有怎样的数量关系？写出你的猜想，并给出证明．
②如图3，在Rt△ABC中，点F为斜边BC的中点，分别以AB，AC为底边，在
外部作等腰三角形ABD和等腰三角形ACE，连接FD，FE，分别交AB，AC于点M，N．试猜想四边形FMAN的形状，并说明理由；
（3）问题解决：
如图4，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE、BG，GE，已知AC=2，AB=5．求GE的长度．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
