
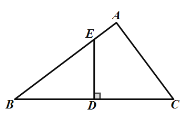
【题目】已知在![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() .
.
(1)求![]() 的度数;
的度数;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)90°(2)1.4
【解析】
(1)连接CE,根据线段垂直平分线的性质转化线段BE到△AEC中,利用勾股定理的逆定理可求∠A度数;
(2)设AE=x,则AC可用x表示,在Rt△ABC中利用勾股定理得到关于x的方程求解AE值.
(1)连接CE,∵D是BC的中点,DE⊥BC,
∴CE=BE.
∵BE2AE2=AC2,
∴AE2+AC2=CE2.
∴△AEC是直角三角形,∠A=90°;
(2)在Rt△BDE中,BE=![]() =5.
=5.
所以CE=BE=5.
设AE=x,则在Rt△AEC中,AC2=CE2AE2,
所以AC2=25x2.
∵BD=4,
∴BC=2BD=8.
在Rt△ABC中,根据BC2=AB2+AC2,
即64=(5+x)2+25x2,
解得x=1.4.
即AE=1.4.


科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 分别与y轴、x轴交于点A、点B,点C的坐标为(-3,0),D为直线AB上一动点,连接CD交y轴于点E.
分别与y轴、x轴交于点A、点B,点C的坐标为(-3,0),D为直线AB上一动点,连接CD交y轴于点E.
(1) 点B的坐标为__________,不等式![]() 的解集为___________
的解集为___________
(2) 若S△COE=S△ADE,求点D的坐标;
(3) 如图2,以CD为边作菱形CDFG,且∠CDF=60°.当点D运动时,点G在一条定直线上运动,请求出这条定直线的解析式.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产某种产品,每件产品的生产成本为25元,出厂价为50元.在生产过程中,平均每生产一件这种产品有0.5m3的污水排出.为净化环境,该厂购买了一套污水处理设备,每处理1m3污水所需原材料费为2元,每月排污设备耗费4000元.
(1)请给出该厂每月的利润与产品件数的函数关系式;
(2)为保证每月盈利30000元,该厂每月至少需生产并销售这种产品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
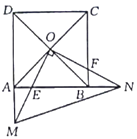
【题目】如图,正方形![]() 的对角线交于点
的对角线交于点![]() 点
点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上(
上(![]() )且
)且![]() ,
,![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,
,![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.
(1)求证:![]() .
.
(2)若正方形![]() 的边长为4,
的边长为4,![]() 为
为![]() 的中点,求
的中点,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
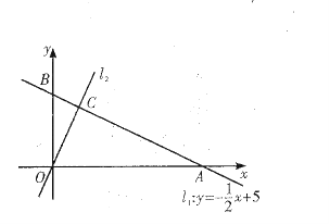
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象
的图象![]() 分别与
分别与![]() 轴交于
轴交于![]() 两点,正比例函数的图象
两点,正比例函数的图象![]() 与
与![]() 交于点
交于点![]()
(1)求![]() 的值及
的值及![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)一次函数![]() 的图象为
的图象为![]() 且
且![]() 不能围成三角形,直接写出
不能围成三角形,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中有2个红球和3个黑球,它们只有颜色上的区别.
(1)从布袋中随机摸出一个球,求摸出红球的概率;
(2)现从布袋中取出一个红球和一个黑球,放入另一个不透明的空布袋中,甲乙两人约定做如下游戏:两人分别从这两个布袋中各随机摸出一个小球,若颜色相同,则甲获胜;若颜色不同,则乙获胜.请用树状图(或列表)的方法表示游戏所有可能的结果,并用概率知识说明这个游戏是否公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新农村社区改造中,有一部分楼盘要对外销售.某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2 , 从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元.已知该楼盘每套楼房面积均为120米2 , 若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价l0%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x( ![]() ,x取整数)之间的函数关系式;
,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一列有理数﹣1,2,﹣3,4,﹣5,6,……,如图所示有序排列.根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰6”中C的位置是有理数_____,2018应排在A,B,C,D,E中的_____位置.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com