
【题目】新农村社区改造中,有一部分楼盘要对外销售.某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2 , 从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元.已知该楼盘每套楼房面积均为120米2 , 若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价l0%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x( ![]() ,x取整数)之间的函数关系式;
,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
【答案】
(1)解:当1≤x≤8时,y=400030(8x)=30x+3760;
当8<x≤23时,y=4000+50(x8)=50x+3600.
∴所求函数关系式为 ![]() (x为正整数)
(x为正整数)
(2)解:当x=16时,
方案一楼房总费用:
w1=120(50×16+3600)×92%-a=485760-a;
方案二楼房总费用:
w2=120(50×16+3600)×90%=475200.
∴当w1<w2时,即485760-a<475200时,a>10560;
当w1=w2时,即485760-a=475200时,a=10560;
当w1>w2时,即485760-a>475200时,a<10560.
因此,当每套赠送装修基金多于10560元时,选择方案一合算;
当每套赠送装修基金等于10560元时,两种方案一样;
当每套赠送装修基金少于10560元时,选择方案二合算
【解析】(1)此题是一道分段函数的问题,①当1≤x≤8时,房屋下降的层数为 (8-x),房屋的销售单价=4000-30×楼层下降的层数得出函数解析式;②当8<x≤23时,房屋上升的层数为 (x-8),然后利用房屋的销售单价=4000+50×楼层上升的层数得出函数解析式;
(2)当x=16时, 方案一楼房总费用=楼层单价×房屋总面积=120(50×16+3600)×92%-a=485760-a; 方案二楼房总费用= 楼层单价×房屋总面120(50×16+3600)×90%=475200. 然后分三类讨论; 方案一>方案二, 方案一=方案二 ; 方案一<方案二;得出赠送装修基金a的取值范围得出答案。


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将一点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这一点的“互换点”,如(﹣3,5)与(5,﹣3)是一对“互换点”.
(1)任意一对“互换点”能否都在一个反比例函数的图象上?为什么?
(2)M、N是一对“互换点”,若点M的坐标为(m,n),求直线MN的表达式(用含m、n的代数式表示);
(3)在抛物线y=x2+bx+c的图象上有一对“互换点”A、B,其中点A在反比例函数y=﹣ ![]() 的图象上,直线AB经过点P(
的图象上,直线AB经过点P( ![]() ,
, ![]() ),求此抛物线的表达式.
),求此抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (k>0)与正比例函数y=ax相交于A(1,k),B(﹣k,﹣1)两点.
(k>0)与正比例函数y=ax相交于A(1,k),B(﹣k,﹣1)两点.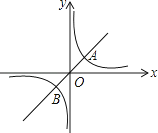
(1)求反比例函数和正比例函数的解析式;
(2)将正比例函数y=ax的图象平移,得到一次函数y=ax+b的图象,与函数![]() (k>0)的图象交于C(x1 , y1),D(x2 , y2),且|x1﹣x2||y1﹣y2|=5,求b的值.
(k>0)的图象交于C(x1 , y1),D(x2 , y2),且|x1﹣x2||y1﹣y2|=5,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
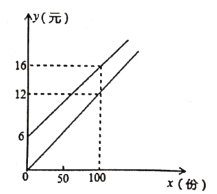
【题目】我校准备实行学案式教学,需印刷若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用![]() (元)与印刷份数
(元)与印刷份数![]() (份)之间的关系如图所式.
(份)之间的关系如图所式.
(1)求出甲、乙两种收费方式的函数关系式;
(2)我校八年级每次需印刷100-450(含100和450)份学案,选择哪种印刷方式较合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为传播“绿色出行,低碳生活”的理念,小贾同学的爸爸从家里出发,骑自行车去图书馆看书,图1表达的是小贾的爸爸行驶的路程![]() (米)与行驶时间
(米)与行驶时间![]() (分钟)的变化关系
(分钟)的变化关系
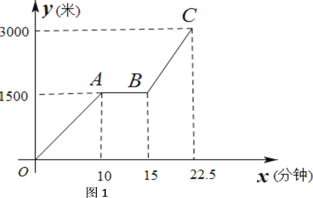
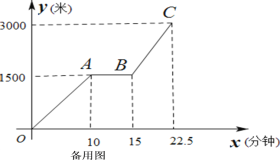
(1)求线段BC所表达的函数关系式;
(2)如果小贾与爸爸同时从家里出发,小贾始终以速度120米/分钟行驶,当小贾与爸爸相距100米是,求小贾的行驶时间;
(3)如果小贾的行驶速度是![]() 米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出
米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若数a使关于x的不等式组 ,有且仅有四个整数解,且使关于y的分式方程
,有且仅有四个整数解,且使关于y的分式方程![]() 有非负数解,则所有满足条件的整数a的值之和是________________.
有非负数解,则所有满足条件的整数a的值之和是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设A= ![]() ÷(a﹣
÷(a﹣ ![]() ).
).
(1)化简A;
(2)当a=3时,记此时A的值为f(3);当a=4时,记此时A的值为f(4);… 解关于x的不等式: ![]() ﹣
﹣ ![]() ≤f(3)+f(4)+…+f(11),并将解集在数轴上表示出来.
≤f(3)+f(4)+…+f(11),并将解集在数轴上表示出来.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com