
【题目】在平面直角坐标系中,将一点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这一点的“互换点”,如(﹣3,5)与(5,﹣3)是一对“互换点”.
(1)任意一对“互换点”能否都在一个反比例函数的图象上?为什么?
(2)M、N是一对“互换点”,若点M的坐标为(m,n),求直线MN的表达式(用含m、n的代数式表示);
(3)在抛物线y=x2+bx+c的图象上有一对“互换点”A、B,其中点A在反比例函数y=﹣ ![]() 的图象上,直线AB经过点P(
的图象上,直线AB经过点P( ![]() ,
, ![]() ),求此抛物线的表达式.
),求此抛物线的表达式.
【答案】
(1)解:不一定,
设这一对“互换点”的坐标为(a,b)和(b,a).
①当ab=0时,它们不可能在反比例函数的图象上,
②当ab≠0时,由 ![]() 可得
可得 ![]() ,即(a,b)和(b,a)都在反比例函数
,即(a,b)和(b,a)都在反比例函数 ![]() (k≠0)的图象上;
(k≠0)的图象上;
(2)解:由M(m,n)得N(n,m),设直线MN的表达式为y=cx+d(c≠0).
则有 ![]() 解得
解得 ![]() ,
,
∴直线MN的表达式为y=﹣x+m+n;
(3)解:设点A(p,q),则 ![]() ,
,
∵直线AB经过点P( ![]() ,
, ![]() ),由(2)得
),由(2)得 ![]() ,
,
∴p+q=1,
∴ ![]() ,
,
解并检验得:p=2或p=﹣1,
∴q=﹣1或q=2,
∴这一对“互换点”是(2,﹣1)和(﹣1,2),
将这一对“互换点”代入y=x2+bx+c得,
∴ ![]() 解得
解得 ![]() ,
,
∴此抛物线的表达式为y=x2﹣2x﹣1.
【解析】(1)设这一对“互换点”的坐标为(a,b)和(b,a).①当ab=0时,它们不可能在反比例函数的图象上,②当ab≠0时,由 ![]() 可得
可得 ![]() ,于是得到结论;(2)把M(m,n),N(n,m)代入y=cx+d,即可得到结论;(3)设点A(p,q),则
,于是得到结论;(2)把M(m,n),N(n,m)代入y=cx+d,即可得到结论;(3)设点A(p,q),则 ![]() ,由直线AB经过点P(
,由直线AB经过点P( ![]() ,
, ![]() ),得到p+q=1,得到q=﹣1或q=2,将这一对“互换点”代入y=x2+bx+c得,于是得到结论.
),得到p+q=1,得到q=﹣1或q=2,将这一对“互换点”代入y=x2+bx+c得,于是得到结论.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.


科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC= ![]() ,反比例函数y=
,反比例函数y= ![]() 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于 .
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 分别与y轴、x轴交于点A、点B,点C的坐标为(-3,0),D为直线AB上一动点,连接CD交y轴于点E.
分别与y轴、x轴交于点A、点B,点C的坐标为(-3,0),D为直线AB上一动点,连接CD交y轴于点E.
(1) 点B的坐标为__________,不等式![]() 的解集为___________
的解集为___________
(2) 若S△COE=S△ADE,求点D的坐标;
(3) 如图2,以CD为边作菱形CDFG,且∠CDF=60°.当点D运动时,点G在一条定直线上运动,请求出这条定直线的解析式.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每一个小正方形边长都是1,每个小格的顶点叫作格点,以格点为顶点分别按下列要求画图.
(1)画出一个周长为24,面积为24的直角三角形;
(2)画出一个周长为20,面积为24的菱形;


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系之中,点O为坐标原点,直线![]() 分别交x、y轴于点B、A,直线
分别交x、y轴于点B、A,直线![]() 与直线
与直线![]() 交于点C.
交于点C.
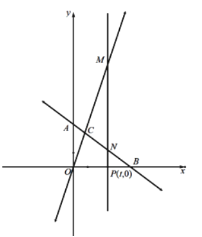
(1)如图1,求点C的坐标.
(2)如图2,点P(t,0)为C点的右侧x轴上一点,过点P作x轴垂线分别交AB、OC于点N、M,若MN=5NP,求t的值.
(3)如图3,点F为平面内任意一点,是否存在y轴正半轴上一点E,使点E、F、M、N围成的四边形为菱形,若存在求出点E坐标;若不存在,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产某种产品,每件产品的生产成本为25元,出厂价为50元.在生产过程中,平均每生产一件这种产品有0.5m3的污水排出.为净化环境,该厂购买了一套污水处理设备,每处理1m3污水所需原材料费为2元,每月排污设备耗费4000元.
(1)请给出该厂每月的利润与产品件数的函数关系式;
(2)为保证每月盈利30000元,该厂每月至少需生产并销售这种产品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新农村社区改造中,有一部分楼盘要对外销售.某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2 , 从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元.已知该楼盘每套楼房面积均为120米2 , 若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价l0%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x( ![]() ,x取整数)之间的函数关系式;
,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com