
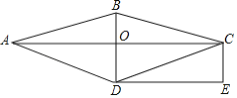
【题目】如图,在菱形![]() 中,对角线
中,对角线![]() 与
与![]() 交于点
交于点![]() .过点
.过点![]() 作
作![]() 的平行线,过点
的平行线,过点![]() 作
作![]() 的平行线,两直线相交于点
的平行线,两直线相交于点![]() .
.
(1)求证:四边形![]() 是矩形;
是矩形;
(2)若![]() ,
,![]() ,则菱形
,则菱形![]() 的面积是 .
的面积是 .
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,点F是射线DC上一动点(不与C,D重合).连接AF并延长交直线BC于点E,交BD于H,连接CH,过点C作CG⊥HC交AE于点G.
(1)若点F在边CD上,如图1.
①证明:∠DAH=∠DCH;
②猜想:△GFC的形状并说明理由.
(2)取DF中点M,连接MG.若MG=2.5,正方形边长为4,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们把对角线互相垂直的四边形叫做垂美四边形.
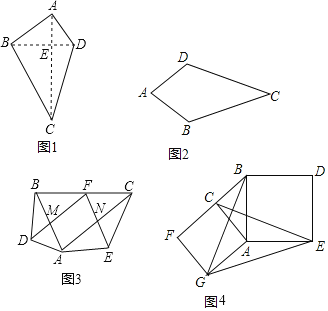
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,那么四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探究:
①如图1,垂美四边形ABCD两组对边AB、CD与BC、AD之间有怎样的数量关系?写出你的猜想,并给出证明.
②如图3,在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在![]() 外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
(3)问题解决:
如图4,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE、BG,GE,已知AC=2,AB=5.求GE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产![]() 两种产品共60件,需购买甲、乙两种材料.生产一件
两种产品共60件,需购买甲、乙两种材料.生产一件![]() 产品需甲种材料4千克;生产一件
产品需甲种材料4千克;生产一件![]() 产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产![]() 产品不少于38件,问符合生产条件的生产方案有哪几种?
产品不少于38件,问符合生产条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件![]() 产品需加工费40元,生产一件
产品需加工费40元,生产一件![]() 产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)?
产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头方向,每次移动1个单位长度,依次得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,1),…,则点A2018的坐标是_____.
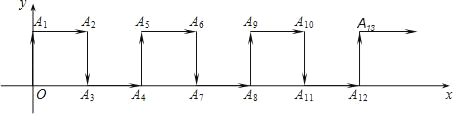
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市对位于笔直公路AC上两个小区A,B的供水路线进行优化改造,供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A,B之间的距离为300(![]() +1)米,求供水站M分别到小区A,B的距离.(结果可保留根号)
+1)米,求供水站M分别到小区A,B的距离.(结果可保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() 所示,在A,B两地间有一车站C,一辆汽车从A地出发经C站匀速驶往B地
所示,在A,B两地间有一车站C,一辆汽车从A地出发经C站匀速驶往B地![]() 如图
如图![]() 是汽车行驶时离C站的路程
是汽车行驶时离C站的路程![]() 千米
千米![]() 与行驶时间
与行驶时间![]() 小时
小时![]() 之间的函数关系的图象.
之间的函数关系的图象.
![]() 填空:
填空:![]() ______km,AB两地的距离为______km;
______km,AB两地的距离为______km;
![]() 求线段PM、MN所表示的y与x之间的函数表达式;
求线段PM、MN所表示的y与x之间的函数表达式;
![]() 求行驶时间x在什么范围时,小汽车离车站C的路程不超过60千米?
求行驶时间x在什么范围时,小汽车离车站C的路程不超过60千米?
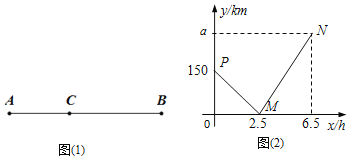
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市委、市政府创建“森林城市”的号召,某中学在校园内计划种植柳树和银杏树.已知购买2棵柳树苗和3棵银杏树苗共需1800元,购买4棵柳树苗和1棵银杏树苗共需1100元.
(1)求每棵柳树苗和每棵银杏树苗各多少钱?
(2)该校计划购买两种树苗共100棵,并且银杏树苗的数量不少于柳树苗的![]() ,请设计出最省钱的购买方案,并说明理由.
,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com