
【题目】如图![]() 所示,在A,B两地间有一车站C,一辆汽车从A地出发经C站匀速驶往B地
所示,在A,B两地间有一车站C,一辆汽车从A地出发经C站匀速驶往B地![]() 如图
如图![]() 是汽车行驶时离C站的路程
是汽车行驶时离C站的路程![]() 千米
千米![]() 与行驶时间
与行驶时间![]() 小时
小时![]() 之间的函数关系的图象.
之间的函数关系的图象.
![]() 填空:
填空:![]() ______km,AB两地的距离为______km;
______km,AB两地的距离为______km;
![]() 求线段PM、MN所表示的y与x之间的函数表达式;
求线段PM、MN所表示的y与x之间的函数表达式;
![]() 求行驶时间x在什么范围时,小汽车离车站C的路程不超过60千米?
求行驶时间x在什么范围时,小汽车离车站C的路程不超过60千米?
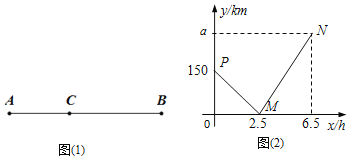
【答案】(1)240 390;(2)PM所表示的函数关系式为:![]() ,MN所表示的函数关系式为:
,MN所表示的函数关系式为:![]() ;(3)
;(3)![]() ,小汽车离车站C的路程不超过60千米.
,小汽车离车站C的路程不超过60千米.
【解析】
(1)根据图象中的数据即可得到A,B两地的距离;
(2)根据函数图象中的数据即可得到两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;
(3)根据题意可以分相遇前和相遇后两种情况进行解答.
解:![]() 由题意和图象可得,
由题意和图象可得,
![]() 千米,
千米,
A,B两地相距:![]() 千米,
千米,
故答案为:240,390
![]() 由图象可得,A与C之间的距离为150km
由图象可得,A与C之间的距离为150km
汽车的速度![]() ,
,
PM所表示的函数关系式为:![]()
MN所表示的函数关系式为:![]()
![]() 由
由![]() 得
得![]() ,解得:
,解得:![]()
由![]() 得
得![]() ,解得:
,解得:![]()
由图象可知当行驶时间满足:![]() ,小汽车离车站C的路程不超过60千米
,小汽车离车站C的路程不超过60千米


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】对于数对(a,b)、(c,d),定义:当且仅当a=c且b=d时,(a,b)=(c,d);并定义其运算如下: (a,b)※(c,d)=(ac﹣bd,ad+bc),如(1,2)※(3,4)=(1×3﹣2×4,1×4+2×3)=(﹣5,10).若(x,y)※(1,﹣1)=(1,3),则xy的值是( )
A.﹣1
B.0
C.1
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠1=∠2,EG平分∠AEC.
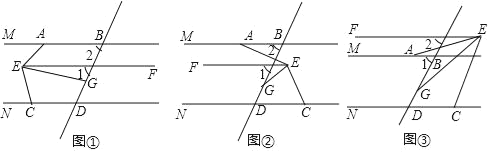
(1)如图①,∠MAE=45°,∠FEG=15°,∠NCE=75°.求证:AB∥CD;
(2)如图②,∠MAE=140°,∠FEG=30°,当∠NCE= °时,AB∥CD;
(3)如图②,请你直接写出∠MAE、∠FEG、∠NCE之间满足什么关系时,AB∥CD;
(4)如图③,请你直接写出∠MAE、∠FEG、∠NCE之间满足什么关系时,AB∥CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
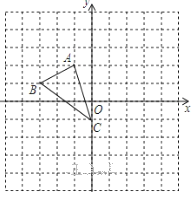
【题目】如图,在平面直角坐标系网格中,△ABC的顶点都在格点上,点C坐标(0,-1).
![]() 作出△ABC 关于原点对称的△A1B1C1,并写出点A1的坐标;
作出△ABC 关于原点对称的△A1B1C1,并写出点A1的坐标;
![]() 把△ABC 绕点C逆时针旋转90°,得△A2B2C2,画出△A2B2C2,并写出点A2的坐标;
把△ABC 绕点C逆时针旋转90°,得△A2B2C2,画出△A2B2C2,并写出点A2的坐标;
(3)直接写出△A2B2C2的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
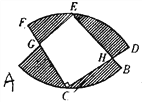
【题目】如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H.且点C是![]() 的中点,若扇形的半径为3.则图中阴影部分的面积等于______.
的中点,若扇形的半径为3.则图中阴影部分的面积等于______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学学习过程中,通常是利用已有的知识与经验,通过对研究对象进行观察、实验、推理、抽象概括,发现数学规律,揭示研究对象的本质特征.比如在学习“同底数幂的乘法法则”过程中,利用有理数的乘方概念和乘法结合律,可由“特殊”抽象概括出“一般”,具体如下22×23=25,23×24=27,22×26=28…→2m2n=2m+n…→aman=am+n(m、n都是正整数)我们亦知: ![]() ,
, ![]() ,
, ![]() ,
, ![]() …
…
(1)请你根据上面的材料,用字母a、b、c归纳出a、b、c(a>b>0,c>0)之间的一个数学关系式.
(2)请尝试说明(1)中关系式的正确性.
(3)试用(1)中你归纳的数学关系式,解释下面生活中的一个现象:“若m克糖水里含有n克糖,再加入k克糖(仍不饱和),则糖水更甜了”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com