【题目】已知等腰三角形的两条边a,b是方程x2－kx＋12=0的两根，另一边c是方程x2－16=0的一个根, 求k的值.
【答案】
或
【解析】试题分析：先解方程x2-16=0，得到c=4，再分两种情况进行讨论：①c=4是底边，那么a=b，由方程x2-kx+12=0的判别式△=0列出方程；②c=4是腰，那么将x=4代入x2-kx+12=0求出k的值.
解：∵c是方程x216=0的一个根，
∴c=4.
分两种情况：
①c=4是底边，
方程x2kx+12=0的判别式△=k24×12=0，
解得k1=
，k2=-
(舍去)，
， 
，4满足三角形三边关系定理，符合题意；
②c=4是腰，
将x=4代入x2kx+12=0，
得424k+12=0，
解得k=7，
∴x27x+12=0，
∴x1=3,x2=4，
4，4，3满足三角形三边关系定理，符合题意。
故k的值为
或7.
科目：初中数学 来源： 题型：
【题目】定义：我们把对角线互相垂直的四边形叫做垂美四边形．
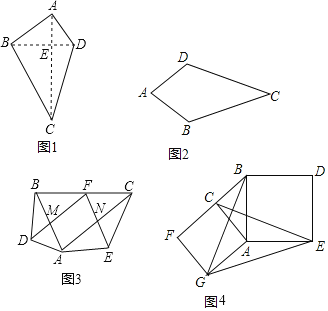
（1）概念理解：如图2，在四边形ABCD中，AB=AD，CB=CD，那么四边形ABCD是垂美四边形吗？请说明理由．
（2）性质探究：
①如图1，垂美四边形ABCD两组对边AB、CD与BC、AD之间有怎样的数量关系？写出你的猜想，并给出证明．
②如图3，在Rt△ABC中，点F为斜边BC的中点，分别以AB，AC为底边，在
外部作等腰三角形ABD和等腰三角形ACE，连接FD，FE，分别交AB，AC于点M，N．试猜想四边形FMAN的形状，并说明理由；
（3）问题解决：
如图4，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE、BG，GE，已知AC=2，AB=5．求GE的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图
所示，在A，B两地间有一车站C，一辆汽车从A地出发经C站匀速驶往B地
如图
是汽车行驶时离C站的路程
千米
与行驶时间
小时之间的函数关系的图象．
填空：
______km，AB两地的距离为______km；
求线段PM、MN所表示的y与x之间的函数表达式；
求行驶时间x在什么范围时，小汽车离车站C的路程不超过60千米？
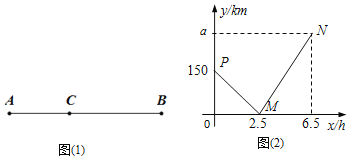
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向，每次移动1个单位，依次得到点P1（0，1），P2（1，1），P3（1，0），P4（1，﹣1），P5（2，﹣1），P6（2，0），…，则点P2018的坐标是________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图所示．
（1）分别写出下列各点的坐标：A′________；B′________；C′________；
（2）说明△A′B′C′由△ABC经过怎样的平移得到；
（3）若点P(a，b)是△ABC内部一点，则平移后△A′B′C′内的对应点P′的坐标为________；
（4）求△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ACB=90，AC=BC=1，E、F为线段AB上两动点，且∠ECF=45°，过点E、F分别作BC、AC的垂线相交于点M，垂足分别为H、G．现有以下结论：①AB=
；②当点E与点B重合时，MH=
；③AF+BE=EF；④MGMH=
，其中正确结论为（ ）
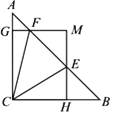
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为响应市委、市政府创建“森林城市”的号召，某中学在校园内计划种植柳树和银杏树．已知购买2棵柳树苗和3棵银杏树苗共需1800元，购买4棵柳树苗和1棵银杏树苗共需1100元．
(1)求每棵柳树苗和每棵银杏树苗各多少钱？
(2)该校计划购买两种树苗共100棵，并且银杏树苗的数量不少于柳树苗的
，请设计出最省钱的购买方案，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
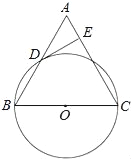
【题目】已知：如图，在△ABC中，BC=AC，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E．
（1）求证：点D是AB的中点；
（2）判断DE与⊙O的位置关系，并证明你的结论；
（3）若⊙O的直径为18，cosB=
，求DE的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com