
【题目】已知如图,在直角坐标系xOy中,点A,点B坐标分别为(﹣1,0),(0, ![]() ),连结AB,OD由△AOB绕O点顺时针旋转60°而得.
),连结AB,OD由△AOB绕O点顺时针旋转60°而得.
(1)求点C的坐标;
(2)△AOB绕点O顺时针旋转60°所扫过的面积;
(3)线段AB绕点O顺时针旋转60°所扫过的面积.
【答案】
(1)解:如图1,过C作CE⊥OA于E,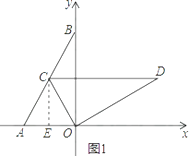
∵点A,点B坐标分别为(﹣1,0),(0, ![]() ),
),
∴OA=1,OB= ![]() ,
,
∵△AOB绕点O顺时针旋转60°得到△COD,
∴∠AOC=∠BOD=60°,AO=OC=1,
∴OE= ![]() OC=
OC= ![]() ,CE=
,CE= ![]() OC=
OC= ![]() ,
,
∴C(﹣ ![]() ,
, ![]() )
)
(2)解:△AOB绕点O顺时针旋转60°所扫过的面积= ![]() +
+ ![]() +
+ ![]() ×
× ![]() =
= ![]() π+
π+ ![]()
(3)解:如图2,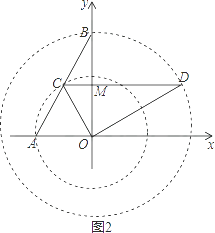
线段AB绕点O顺时针旋转60°所扫过的面积═( ![]() ﹣1×
﹣1× ![]() )+(
)+(![]()
![]() )+
)+![]() (
( ![]() ﹣
﹣ ![]() )=
)= ![]() .
.
【解析】(1)根据题意可作辅助线,过C作CE⊥OA于E,由旋转的性质可得∠AOC=∠BOD=60°,AO=OC=1,再由直角三角形中,30度角所对的直角边等于斜边的一半可求得OE的长,在直角三角形CEO中,用锐角三角函数可求CE的长,根据点C在第二象限可写出点C的坐标。
(2)由题意结合图形可得,△AOB绕点O顺时针旋转60°所扫过的面积=扇形AOC的面积+扇形BOD的面积+三角形BOC的面积。
(3)由题意结合图形可得,线段AB绕点O顺时针旋转60°所扫过的面积═扇形AOC的面积-三角形AOC的面积+扇形BOD的面积-三角形DOM的面积+三角形BCM的面积。扇形面积=n![]()
![]()
![]() 360.
360.


科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (k>0)与正比例函数y=ax相交于A(1,k),B(﹣k,﹣1)两点.
(k>0)与正比例函数y=ax相交于A(1,k),B(﹣k,﹣1)两点.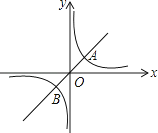
(1)求反比例函数和正比例函数的解析式;
(2)将正比例函数y=ax的图象平移,得到一次函数y=ax+b的图象,与函数![]() (k>0)的图象交于C(x1 , y1),D(x2 , y2),且|x1﹣x2||y1﹣y2|=5,求b的值.
(k>0)的图象交于C(x1 , y1),D(x2 , y2),且|x1﹣x2||y1﹣y2|=5,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为传播“绿色出行,低碳生活”的理念,小贾同学的爸爸从家里出发,骑自行车去图书馆看书,图1表达的是小贾的爸爸行驶的路程![]() (米)与行驶时间
(米)与行驶时间![]() (分钟)的变化关系
(分钟)的变化关系
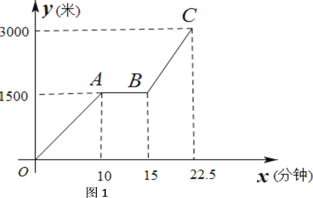
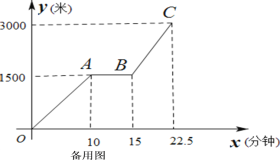
(1)求线段BC所表达的函数关系式;
(2)如果小贾与爸爸同时从家里出发,小贾始终以速度120米/分钟行驶,当小贾与爸爸相距100米是,求小贾的行驶时间;
(3)如果小贾的行驶速度是![]() 米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出
米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若数a使关于x的不等式组 ,有且仅有四个整数解,且使关于y的分式方程
,有且仅有四个整数解,且使关于y的分式方程![]() 有非负数解,则所有满足条件的整数a的值之和是________________.
有非负数解,则所有满足条件的整数a的值之和是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
(1)写出A、B、C的坐标.
(2)以原点O为中心,将△ABC围绕原点O逆时针旋转180°得到△A1B1C1,画出△A1B1C1.
(3)求(2)中C到C1经过的路径以及OB扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,点F是射线DC上一动点(不与C,D重合).连接AF并延长交直线BC于点E,交BD于H,连接CH,过点C作CG⊥HC交AE于点G.
(1)若点F在边CD上,如图1.
①证明:∠DAH=∠DCH;
②猜想:△GFC的形状并说明理由.
(2)取DF中点M,连接MG.若MG=2.5,正方形边长为4,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在矩形ABCD中,对角线AC与BD相交于点O,过点C作BD的平行线,过点D作AC的平行线,两线交于点P.
①求证:四边形CODP是菱形.
②若AD=6,AC=10,求四边形CODP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设A= ![]() ÷(a﹣
÷(a﹣ ![]() ).
).
(1)化简A;
(2)当a=3时,记此时A的值为f(3);当a=4时,记此时A的值为f(4);… 解关于x的不等式: ![]() ﹣
﹣ ![]() ≤f(3)+f(4)+…+f(11),并将解集在数轴上表示出来.
≤f(3)+f(4)+…+f(11),并将解集在数轴上表示出来.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头方向,每次移动1个单位长度,依次得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,1),…,则点A2018的坐标是_____.
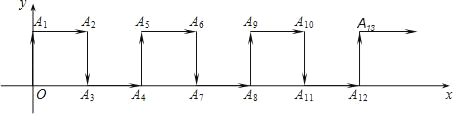
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com