
【题目】如图,已知△BAD≌△EBC,∠BAD=∠BCE=90°,∠ABD=∠BEC=30°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)如图1,当A,B,E三点在同一直线上时,判断AC与CN数量关系为________;
(2)将图1中△BCE绕点B逆时针旋转到图2位置时,(1)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由;
(3)将图1中△BCE绕点B逆时针旋转一周,旋转过程中△CAN能否为等腰直角三角形?若能,直接写出旋转角度;若不能,说明理由.

【答案】(1)AC=CN;(2)成立,证明见解析;(3)△CAN能成为等腰直角三角形,此时旋转角为60°.
【解析】
(1)根据平行线的性质可得∠NEM=∠ADM,由中点的定义可得DM=EM,利用ASA可证明△ADM≌△NEM,可得AD=NE,根据全等三角形的性质可得AD=BC,AB=CE,根据等量代换的NE=BC,由∠BEC=30°,可得∠NEC=∠ABC=120°,利用SAS可证明△ABC≌△NEC,即可证明AC=NC,可得答案;
(2)设旋转角为α,同(1)可证明△MEN≌△MDA,可得NE=BC,可利用α表示出∠ABC、∠DBE,根据平行线的性质可用α表示出∠CEN,即可得出∠ABC=∠CEN,利用SAS可证明△ABC≌△CEN,即可证明(1)中结论依然成立;
(3)由△CAN为等腰直角三角形,AC=CN可得∠CAN=90°,设旋转角为![]() ,可知旋转过程中∠ABC=120°+
,可知旋转过程中∠ABC=120°+![]() ,可得∠ABC=180°时,∠CAN=90°,进而求出
,可得∠ABC=180°时,∠CAN=90°,进而求出![]() 的度数即可.
的度数即可.
(1)AC与CN数量关系为:AC=CN.理由如下:
∵△BAD≌△BCE,
∴BC=AD,EC=AB,
∵EN∥AD,∠DAB=90°,
∴∠MEN=∠MDA.∠BEN=90°,
∵∠BEC=30°,∠BCE=90°,
∴∠CEN=120°,∠ABC=120°,
∴∠CEN=∠ABC,
∵M为DE的中点,
∴MD=ME,
在△MEN与△MDA中,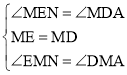 ,
,
∴△MEN≌△MDA(ASA),
∴EN=AD,
∴EN=BC.
在△ABC与△CEN中,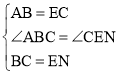 ,
,
∴△ABC≌△CEN(SAS),
∴AC=CN.
(2)结论仍然成立.理由如下:
与(1)同理,可证明△MEN≌△MDA,
∴EN=BC.
设旋转角为α,
∴∠ABC=120°+α,
∵∠ABD=30°,
∴∠DBE=150°-α,
∵BD=BE,
∴∠BED=∠BDE=![]() (180°-∠DBE)=15°+
(180°-∠DBE)=15°+![]() α,
α,
∵EN∥AD,
∴∠MEN=∠MDA=∠ADB+∠BDE=60°+(15°+![]() α)=75°+
α)=75°+![]() α,
α,
∴∠CEN=∠CEB+∠BED+∠MEN=30°+(15°+![]() α)+(75°+
α)+(75°+![]() α)=120°+α,
α)=120°+α,
∴∠ABC=∠CEN,
在△ABC与△CEN中,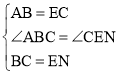 ,
,
∴△ABC≌△CEN(SAS),
∴AC=CN.
(3)如图,设旋转角为![]() ,
,
∵图1中∠ABC=120°,
∴旋转过程中,∠ABC=120°+![]() ,
,
∵△CAN为等腰直角三角形,AC=CN,
∴∠CAN=90°,
∴当∠ABC=180°时,∠CAN=90°,即点A、B、C在一条直线上,点N、E、C在一条直线上.
∴![]() =180°-120°=60°
=180°-120°=60°

∴△CAN能成为等腰直角三角形,此时旋转角为60°.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a、b满足![]() +|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
(1)a=______________,b=_____________,点B的坐标为_______________;
(2)当点P移动4秒时,请指出点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若数a使关于x的不等式组 ,有且仅有四个整数解,且使关于y的分式方程
,有且仅有四个整数解,且使关于y的分式方程![]() 有非负数解,则所有满足条件的整数a的值之和是________________.
有非负数解,则所有满足条件的整数a的值之和是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在圆心角为135°的扇形OAB中,半径OA=2cm,点C,D为 ![]() 的三等分点,连接OC,OD,AC,CD,BD,则图中阴影部分的面积为cm2 .
的三等分点,连接OC,OD,AC,CD,BD,则图中阴影部分的面积为cm2 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,点F是射线DC上一动点(不与C,D重合).连接AF并延长交直线BC于点E,交BD于H,连接CH,过点C作CG⊥HC交AE于点G.
(1)若点F在边CD上,如图1.
①证明:∠DAH=∠DCH;
②猜想:△GFC的形状并说明理由.
(2)取DF中点M,连接MG.若MG=2.5,正方形边长为4,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
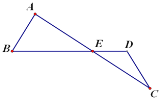
【题目】如图,在△ABE中,∠B=60°,AB=8,C、D分别是△ABE的边AE延长线上和边BE延长线上两点,连接CD,∠A-∠C=60°,AB=CD,DE=6,则线段AC的长度等于______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产![]() 两种产品共60件,需购买甲、乙两种材料.生产一件
两种产品共60件,需购买甲、乙两种材料.生产一件![]() 产品需甲种材料4千克;生产一件
产品需甲种材料4千克;生产一件![]() 产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产![]() 产品不少于38件,问符合生产条件的生产方案有哪几种?
产品不少于38件,问符合生产条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件![]() 产品需加工费40元,生产一件
产品需加工费40元,生产一件![]() 产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)?
产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低(成本=材料费+加工费)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com