
【题目】如图,在圆心角为135°的扇形OAB中,半径OA=2cm,点C,D为 ![]() 的三等分点,连接OC,OD,AC,CD,BD,则图中阴影部分的面积为cm2 .
的三等分点,连接OC,OD,AC,CD,BD,则图中阴影部分的面积为cm2 . 
【答案】![]() π﹣3
π﹣3 ![]()
【解析】解:如图作DH⊥OB于H.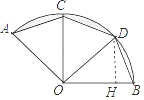
∵点C,D为 ![]() 的三等分点,∠AOB=135°,
的三等分点,∠AOB=135°,
∴∠AOC=∠COD=∠DOB=45°,
∴△ODH是等腰直角三角形,△AOC≌△COD≌△DOB,
∵OD=2,
∴DH=OH= ![]() ,
,
∴S△ODB= ![]() OBDH=
OBDH= ![]() ,
,
∴S△AOC=S△COD=S△DOB= ![]() ,
,
∴S阴= ![]() ﹣3S△DOB=(
﹣3S△DOB=( ![]() π﹣3
π﹣3 ![]() )cm2 ,
)cm2 ,
故答案为( ![]() π﹣3
π﹣3 ![]() )cm2 .
)cm2 .
根据题意可作辅助线,过点D作DH⊥OB于H,由点C,D为 弧 A B 的三等分点可得△AOC≌△COD≌△DOB,所以S阴 =扇形AOB的面积-3![]() S△DOB, 而扇形AOB的面积=n
S△DOB, 而扇形AOB的面积=n![]()
![]()
![]() 360,在三角形DOB中根据已知条件可求高DH,代入上式计算即可求解。
360,在三角形DOB中根据已知条件可求高DH,代入上式计算即可求解。


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里共有2个黄球和3个白球,每个球除颜色外都相同,小亮从袋子中任意摸出一个球,结果是白球,则下面关于小亮从袋中摸出白球的概率和频率的说明正确的是( )
A. 小亮从袋中任意摸出一个球,摸出白球的概率是1
B. 小亮从袋中任意摸出一个球,摸出白球的概率是0
C. 在这次实验中,小亮摸出白球的频率是1
D. 由这次实验的频率去估计小亮从袋中任意摸出一个球,摸出白球的概率是1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() (如图),点
(如图),点![]() 分别在边
分别在边![]() 上,且四边形
上,且四边形![]() 是菱形
是菱形
(1)请使用直尺与圆规,分别确定点![]() 的具体位置(不写作法,保留画图痕迹);
的具体位置(不写作法,保留画图痕迹);
(2)如果![]() ,点
,点![]() 在边
在边![]() 上,且满足
上,且满足![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(3)当![]() 时,求
时,求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
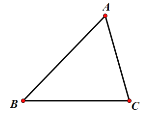
【题目】如图,已知△BAD≌△EBC,∠BAD=∠BCE=90°,∠ABD=∠BEC=30°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)如图1,当A,B,E三点在同一直线上时,判断AC与CN数量关系为________;
(2)将图1中△BCE绕点B逆时针旋转到图2位置时,(1)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由;
(3)将图1中△BCE绕点B逆时针旋转一周,旋转过程中△CAN能否为等腰直角三角形?若能,直接写出旋转角度;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,点D是边AB的中点,点E在边BC上,AE=BE,点M是AE的中点,联结CM,点G在线段CM上,作∠GDN=∠AEB交边BC于N.

(1)如图2,当点G和点M重合时,求证:四边形DMEN是菱形;
(2)如图1,当点G和点M、C不重合时,求证:DG=DN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如 图,在边长为3 cm的正方形ABCD中,点E为BC边上的任意一点,AF⊥AE,AF交CD的延长线于F,则四边形AFCE的面积为_____cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形DEBF是平行四边形,A、C在直线EF上且AE=CF.
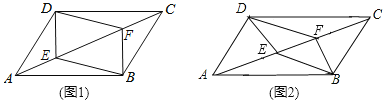
(1)求证:四边形ABCD是平行四边形;
(2)在不添加任何辅助线的条件下,请直接写出图中所有与△DFC面积相等的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两家汽车销售公司根据近几年的销售量分别制作了如图所示的统计图,从2014~2018年,这两家公司中销售量增长较快的是_____公司(填“甲”或“乙”).
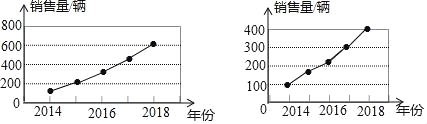
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com