
【题目】先阅读下面的材料,然后解答问题.通过计算,发现方程:
![]() 的解为
的解为![]() ,
,![]() ;
;
![]() 的解为
的解为![]() ,
,![]() ;
;
![]() 的解为
的解为![]() ,
,![]() ;
;
……
(1)观察上述方程的解,猜想关于![]() 的方程
的方程![]() 的解是_____.
的解是_____.
(2)根据上面的规律,猜想关于![]() 的方程
的方程![]() 的解是_______.
的解是_______.
(3)类似地,关于![]() 的方程
的方程![]() 的解是______.
的解是______.
(4)请利用上述规律求关于![]() 的方程
的方程![]() 的解.
的解.
科目:初中数学 来源: 题型:
【题目】一项工程,乙队单独完成比甲队单独完成需多用16天,甲队单独做3天的工作量乙队单独做需要5天才能完成.
(1)甲,乙两队单独完成此项工程各需几天?
(2)该项工程先由甲,乙两队合作,再由甲队单独完成,若完成此项工程不超过18天,甲乙两队至少合作几天?
查看答案和解析>>
科目:初中数学 来源: 题型:
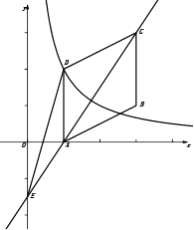
【题目】(本题满分10分)如图,在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),双曲线y=![]() (k≠0,x>0)过点D.
(k≠0,x>0)过点D.
(1)求此双曲线的解析式;
(2)作直线AC交y轴于点E,连结DE,求△ CDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)读读做做:教材中有这样的问题,观察下面的式子,探索它们的规律,![]() =1-
=1-![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ……用正整数n表示这个规律是______;
……用正整数n表示这个规律是______;
(2)问题解决:一容器装有1L水,按照如下要求把水倒出:第一次倒出![]() L水,第二次倒出的水量是
L水,第二次倒出的水量是![]() L水的
L水的![]() ,第三次倒出的水量是
,第三次倒出的水量是![]() L水的
L水的![]() ,第四次倒出的水量是
,第四次倒出的水量是![]() L水的
L水的![]() ,……,第n+1次倒出的水量是
,……,第n+1次倒出的水量是![]() L水的
L水的![]() ,……,按照这种倒水方式,这1L水能否倒完?
,……,按照这种倒水方式,这1L水能否倒完?
(3)拓展探究:①解方程:![]() +
+![]() +
+![]() +
+![]() =
=![]() ;
;
②化简:![]() +
+![]() +
+![]() …+
…+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑经销商计划购进一批电脑机箱和液晶显示器,若购电脑机箱10台和液液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 、
、![]() 重合),以
重合),以![]() 为边在
为边在![]() 右侧作等腰直角三角形
右侧作等腰直角三角形![]() ,使
,使![]() ,连接
,连接![]() .
.
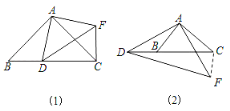
(1)如图1,当点![]() 在线段
在线段![]() 上时;证明
上时;证明
①![]()
②![]()
(2)如图2,当点![]() 在线段
在线段![]() 的延长线上时,结论(1)中的①、②是否仍然成立?若成立,请给予证明:若不成立,请你写出正确结论再给予证明.
的延长线上时,结论(1)中的①、②是否仍然成立?若成立,请给予证明:若不成立,请你写出正确结论再给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。设每件商品降价![]() 元。据此规律,请回答:
元。据此规律,请回答:
(1)商场日销售量增加_____件,每件商品盈利_____元(用含![]() 的代数式表示)。
的代数式表示)。
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边长为4,对角线AC、BD交于点M.
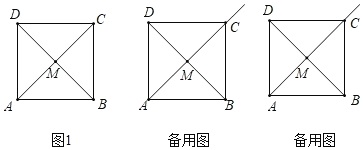
(1)直接写出AM= ;
(2)P是射线AM上的一点,Q是AP的中点,设PQ=x.
①AP= ,AQ= ;
②以PQ为对角线作正方形,设所作正方形与△ABD公共部分的面积为S,用含x的代数式表示S,并写出相应的x的取值范围.(直接写出,不需要写过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com