
【题目】某电器城经销A型号彩电,今年四月份每台彩电售价为2000元,与去年同期相比,结果卖出彩电的数量相同,但去年销售额为5万元,今年销售额只有4万元.
(1)问去年四月份每台A型号彩电售价是多少元?
(2)为了改善经营,电器城决定再经销B型号彩电.已知A型号彩电每台进货价为1800元,B型号彩电每台进货价为1500元,电器城预计用不多于![]() 万元且不少于
万元且不少于![]() 万元的资金购进这两种彩电共20台,问有哪几种进货方案?
万元的资金购进这两种彩电共20台,问有哪几种进货方案?
(3)电器城准备把A型号彩电继续以原价每台2000元的价格出售,B型号彩电以每台1800元的价格出售,在这批彩电全部卖出的前提下,如何进货才能使电器城获利最大?最大利润是多少?
【答案】(1)2500元;(2)方案一:购进A型号彩电7台、B型号彩电13台;方案二:购进A型号彩电8台、B型号彩电12台;方案三:购进A型号彩电9台、B型号彩电11台;方案四:购进A型号彩电10台、B型号彩电10台;(3)当购进A型号彩电7台、B型号彩电13台时,电器城获得的利润最大,最大利润为5300元
【解析】
(1)设去年四月份每台A型号彩电售价是a元,根据两年四月份卖出彩电的数量相同,列方程求解;
(2)设A型号彩电购进x台,则B型号彩电购进(20-x)台,购进共需1800x+1500(20-x)元,根据购进的资金范围,列不等式组求解;
(3)设A型号彩电购进x台,则B型号彩电购进(20-x)台,则利润w=(2000-1800)x+(1800-1500)(20-x),根据一次函数的增减性求最大利润.
解:(1)设去年四月份每台A型号彩电售价![]() 元,依题意:
元,依题意:
![]()
解得:![]() .
.
经检验,![]() 是原方程的解.
是原方程的解.
∴![]() .
.
答:去年四月份每台A型号彩电售价是2500元.
(2)设电器城在此次进货中,购进A型号彩电![]() 台,则B型号彩电
台,则B型号彩电![]() 台,依题意:
台,依题意:
![]()
解得:![]() .
.
由于![]() 只取非负整数,所以
只取非负整数,所以![]() ,8,9,10.
,8,9,10.
所以电器城在此次进货中,共有4种进货方案,分别是:
方案一:购进A型号彩电7台、B型号彩电13台;
方案二:购进A型号彩电8台、B型号彩电12台;
方案三:购进A型号彩电9台、B型号彩电11台;
方案四:购进A型号彩电10台、B型号彩电10台.
(3)设电器城获得的利润为![]() 元,则
元,则![]() 与
与![]() 的函数关系式为:
的函数关系式为:
![]()
∵![]() ,
,![]() 随
随![]() 的增大而减小,且
的增大而减小,且![]() ,8,9,10.
,8,9,10.
∴当![]() 时,
时,![]() 可取得最大值,
可取得最大值,![]() .
.
因此,当购进A型号彩电7台、B型号彩电13台时,电器城获得的利润最大,最大利润为5300元


科目:初中数学 来源: 题型:
【题目】如图:已知点A、B是反比例函数y=﹣![]() 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校书法兴趣小组准备到文具店购买A、B两种类型的毛笔,文具店的销售方法是:一次性购买A型毛笔不超过20支时,按零售价销售;超过20支时,超过部分每支比零售价低0.4元,其余部分仍按零售价销售.一次性购买B型毛笔不超过15支时,按零售价销售;超过15支时,超过部分每支比零售价低0.6元,其余的部分仍按零售价销售.
(1)如果全组共有20名同学,若每人各买1支A型毛笔和2支B型毛笔,共支付145元;若每人各买2支A型毛笔和1支B型毛笔,共支付129元,这家文具店的A、B型毛笔的零售价各是多少?
(2)为了促销,该文具店对A型毛笔除了原来的销售方法外,同时又推出了一种新的销售方法:无论购买多少支,一律按原零售价(即(1)中所求得的A型毛笔的零售价)90%出售.现要购买A型毛笔a支(a>40),在新的销售方法和原来的销售方法中,应选择哪种方法购买花钱较少并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林的门票每张10元,一次使用,考虑到人们的不同需求,也为了吸引更多的游客,该园林除保留原来的售票方法外,还推出了一种“购买个人年票”的售票方法(个人年票从购买日起,可供持票者使用一年).年票分A、B、C三类:A类年票每张120元,持票者进入园林时,无需再用门票;B类年票每张60元,持票者进入该园林时,需再购买门票,每次2元;C类年票每张40元,持票者进入该园林时,需再购买门票,每次3元.
(1)如果只选择一种购买门票的方式,并且计划在一年中用不多于80元花在该园林的门票上,试通过计算,找出可进入该园林次数最多的购票方式,
(2)一年中进入该园林至少超过______________次时,购买A类年票最合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种旅游纪念品,第一周的营业额为200元,第二周该商店对纪念品打8折销售,结果销售量增加3件,营业额增加了40%.
(1)求该商店第二周的营业额;
(2)求第一周该种纪念品每件的销售价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.
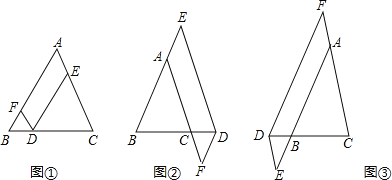
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“蘑菇石”是我国著名的自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1890m.如图,DE∥BC,BD=1800m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m,可参考数据sin29°≈0.4848,sin80°≈0.9848,cos29°≈0.8746,cos80°≈0.1736)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内,如图,在平行四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 边上任意一点,连接
边上任意一点,连接![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() .
.
(![]() )当
)当![]() 时,求
时,求![]() 的大小.
的大小.
(![]() )当
)当![]() 时,求点
时,求点![]() 与点
与点![]() 间的距离(结果保留根号).
间的距离(结果保留根号).
(![]() )若点
)若点![]() 恰好落在平行四边形
恰好落在平行四边形![]() 的边所在的条直线上,直接写出
的边所在的条直线上,直接写出![]() 旋转到
旋转到![]() 所扫过的面积(结果保留
所扫过的面积(结果保留![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3![]() 、7
、7![]() 、9
、9![]() ;乙盒子中装有4张卡片,卡片上分别写着2
;乙盒子中装有4张卡片,卡片上分别写着2![]() 、4
、4![]() 、6
、6![]() 、8
、8![]() ;盒子外有一张写着5
;盒子外有一张写着5![]() 的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com