
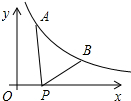
 如图所示,已知A(1,y1),B(2,y2)为反比例函数y=$\frac{2}{x}$图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大值时,点P的坐标是( )
如图所示,已知A(1,y1),B(2,y2)为反比例函数y=$\frac{2}{x}$图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大值时,点P的坐标是( )| A. | (3,0) | B. | ($\frac{7}{2}$,0) | C. | ($\frac{5}{3}$,0) | D. | ($\frac{5}{2}$,0) |
分析 求出A、B的坐标,设直线AB的解析式是y=kx+b,把A、B的坐标代入求出直线AB的解析式,根据三角形的三边关系定理得出在△ABP中,|AP-BP|<AB,延长AB交x轴于P′,当P在P′点时,PA-PB=AB,此时线段AP与线段BP之差达到最大,求出直线AB于x轴的交点坐标即可.
解答 解:∵把A(1,y1),B(2,y2)代入反比例函数y=$\frac{2}{x}$得:y1=2,y2=1,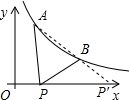
∴A(1,2),B(2,1),
∵在△ABP中,由三角形的三边关系定理得:|AP-BP|<AB,
∴延长AB交x轴于P′,当P在P′点时,PA-PB=AB,
即此时线段AP与线段BP之差达到最大,
设直线AB的解析式是y=kx+b,
把A、B的坐标代入得:$\left\{\begin{array}{l}{k+b=2}\\{2k+b=1}\end{array}\right.$,
解得:k=-1,b=3,
∴直线AB的解析式是y=-x+3,
当y=0时,x=3,
即P(3,0).
故选A.
点评 本题主要考查了反比例函数的综合题的知识,熟练掌握三角形的三边关系定理和用待定系数法求一次函数的解析式,解此题的关键是确定P点的位置,题目比较好,但有一定的难度.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | y=2(x-5)2+1 | B. | y=2(x-5)2-1 | C. | y=2(x+5)2-1 | D. | y=2(x+5)2+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.2×105 | B. | 1.2×105 | C. | 1.3×105 | D. | 1.3×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
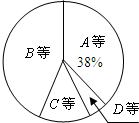 某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.| 等第 | 成绩(得分) | 频数(人数) | 频率 |
| A | 10分 | 7 | 0.14 |
| 9分 | x | 0.24 | |
| B | 8分 | 15 | 0.30 |
| 7分 | 8 | 0.16 | |
| C | 6分 | 4 | 0.08 |
| 5分 | 1 | y | |
| D | 5分以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com