
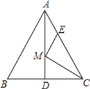
【题目】如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是边AC上一点,若AE=2,则EM+CM的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
在AB上取AE′=AE,连接CE′,过点E′作E′F⊥BC由等边三角形的性质可知:AB=AC=BC=6,∠B=60°,然后证明△AE′M≌△AEM,从而得到E′M=EM,由两点之间线段最短可知:当E′、M、C在一条直线上时,EM+MC有最小值,在Rt△E′BF中,可求得BF=2,E′F=![]() ,最后在Rt△E′FC中,由勾股定理求E′C的长即可.
,最后在Rt△E′FC中,由勾股定理求E′C的长即可.
解:如图所示,在AB上取AE′=AE,连接CE′,过点E′作E′F⊥BC.
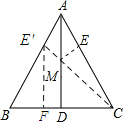
∵△ABC为等边三角形,
∴AB=AC=BC=6.
∵AB=AC,AD是BC边上的中线,
∴∠BAD=∠CAD.
在△AE′M和△AEM中,
 ,
,
∴△AE′M≌△AEM,
∴E′M=EM.
由两点之间线段最短可知:当E′、M、C在一条直线上时,EM+MC有最小值.
∵AE=2, ∴BE′=AB-AE′=4
在Rt△E′BF中,∠B=60°,
∴ ![]() ,
,![]() .
.
∴BF=![]() BE′=
BE′=![]() ×4=2,E′F=
×4=2,E′F= ![]() BE′=
BE′=![]() ×4=
×4=![]() .
.
∴FC=BC-BF=4.
在Rt△E′FC中,
E′C![]() .
.
∴EM+MC=![]() .
.
故选:C.


科目:初中数学 来源: 题型:
【题目】某校开展以感恩教育为主题的艺术活动,举办了四个项目的比赛,它们分别是演讲、唱歌、书法、绘画。要求每位同学必须参加,且限报一项活动。以九年级(1)班为样本进行统计,并将统计结果绘成如图1、图2所示的两幅统计图。请你结合图示所给出的信息解答下列问题。

(1)求出参加绘画比赛的学生人数占全班总人数的百分比?
(2)求出扇形统计图中参加书法比赛的学生所在扇形圆心角的度数?
(3)若该校九年级学生有600人,请你估计这次艺术活动中,参加演讲和唱歌的学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两同学用两枚质地均匀的骰子作游戏,规则如下:每人随机掷两枚骰子一次(若掷出的两枚骰子摞在一起,则重掷),点数和大的获胜;点数和相同为平局.
根据上述规则,解答下列问题;
(1)随机掷两枚骰子一次,用列表法求点数和为8的概率;
(2)甲先随机掷两枚骰子一次,点数和是7,求乙随机掷两枚骰子一次获胜的概率.
(骰子:六个面分别有1、2、3、4、5、6个小圆点的立方块.点数和:两枚骰子朝上的点数之和)
查看答案和解析>>
科目:初中数学 来源: 题型:
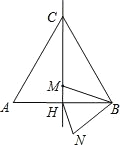
【题目】如图,在边长为 2a 的等边△ABC 中,M 是高 CH 所在直线上的一个动点, 连接 BM,将线段 BM 绕点 B 逆时针旋转 60°得到 BN,连接 HN,则在点 M 运动的过程中,线段 BN 长度的最小值为___________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
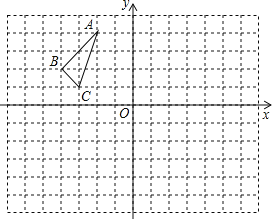
【题目】![]() 在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图:
在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图:
(1)画出![]() 关于原点
关于原点![]() 的中心对称图形
的中心对称图形![]() ;
;
(2)画出将![]() 绕点
绕点![]() 顺时针方向旋转90°得到的
顺时针方向旋转90°得到的![]() .
.
(3)设![]() 为
为![]() 边上一点,在
边上一点,在![]() 上与点
上与点![]() 对应的点是
对应的点是![]() .则点
.则点![]() 坐标为__________.
坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3个完全相同的小球,把它们分别标号为1,2,3,放在一个口袋中,随机地摸出一个小球不放回,再随机地摸出一个小球.
(1) 采用树形图法(或列表法)列出两次摸球出现的所有可能结果;
(2) 求摸出的两个球号码之和等于5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖在二次函数y=2x2+4x+5的图象上,依横坐标找到三点(-1,y1),(![]() ,y2), (-3
,y2), (-3![]() ,y3),则你认为y1,y2,y3的大小关系应为( )
,y3),则你认为y1,y2,y3的大小关系应为( )
A.y1>y2>y3B.y2>y3>y1C.y3>y1>y2D.y3>y2>y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某店只销售某种进价为40元/kg的产品,已知该店按60元kg出售时,每天可售出100kg,后来经过市场调查发现,单价每降低1元,则每天的销售量可增加10kg.
(1)若单价降低2元,则每天的销售量是_____千克,每天的利润为_____元;若单价降低x元,则每天的销售量是_____千克,每天的利润为______元;(用含x的代数式表示)
(2)若该店销售这种产品计划每天获利2240元,单价应降价多少元?
(3)当单价降低多少元时,该店每天的利润最大,最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com