
【题目】完成以下证明,并在括号内填写理由. 已知:如图所示,∠1=∠2,∠A=∠3.
求证:∠ABC+∠4+∠D=180°.
证明:∵∠1=∠2
∴∥()
∴∠A=∠4()
∠ABC+∠BCE=180°()
即∠ABC+∠ACB+∠4=180°
∵∠A=∠3
∴∠3=
∴∥
∴∠ACB=∠D()
∴∠ABC+∠4+∠D=180°.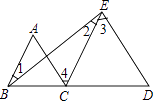
【答案】AB;CE;内错角相等,两直线平行;两直线平行,内错角相等;两直线平行,同旁内角互补;∠4;AC;DE;两直线平行,同位角相等
【解析】证明:∵∠1=∠2, ∴AB∥CE(内错角相等,两直线平行),
∴∠A=∠4(两直线平行,内错角相等),
∠ABC+∠BCE=180°(两直线平行,同旁内角互补),
即∠ABC+∠ACB+∠4=180°,
∵∠A=∠3,
∴∠3=∠4,
∴AC∥DE
∴∠ACB=∠D(两直线平行,同位角相等),
∴∠ABC+∠4+∠D=180°,
所以答案是:AB,CE,内错角相等,两直线平行,两直线平行,内错角相等,两直线平行,同旁内角互补,∠4,AC,DE,两直线平行,同位角相等,
【考点精析】掌握平行线的判定与性质是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


科目:初中数学 来源: 题型:
【题目】如图a是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图b的形状,拼成一个正方形. 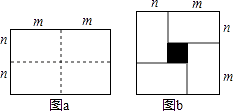
(1)图b中的阴影部分面积为;
(2)观察图b,请你写出三个代数式(m+n)2 , (m﹣n)2 , mn之间的等量关系是;
(3)若x+y=﹣6,xy=2.75,利用(2)提供的等量关系计算x﹣y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在大课间活动中,同学们积极参加体育锻炼.小明在全校随机抽取一部分同学就“我最喜爱的体育项目”进行了一次抽样调查.下面是他通过收集的数据绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
(1)小明共抽取________名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“立定跳远”部分对应的圆心角的度数是_____. ;
(4)若全校共有2130名学生,请你估算“其他”部分的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某学校初四年纪学生每周平均课外阅读时间的情况,随机抽查了该学校初四年级m名同学,对其每周平均课外阅读时间进行统计,绘制了如下条形统计图(图一)和扇形统计图(图二):
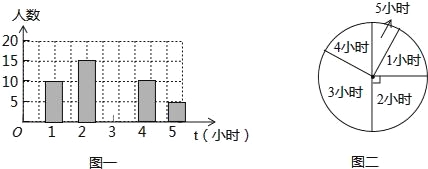
(1)根据以上信息回答下列问题:
①求m值.
②求扇形统计图中阅读时间为5小时的扇形圆心角的度数.
③补全条形统计图.
(2)直接写出这组数据的众数、中位数,求出这组数据的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论中:①若a=b,则 ![]() =
= ![]() ,②在同一平面内,若a⊥b,b∥c,则a⊥c;③直线外一点到直线的垂线段叫点到直线的距离;④|
,②在同一平面内,若a⊥b,b∥c,则a⊥c;③直线外一点到直线的垂线段叫点到直线的距离;④| ![]() ﹣2|=2﹣
﹣2|=2﹣ ![]() ,正确的个数有( )
,正确的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
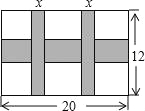
【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的![]() ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com