
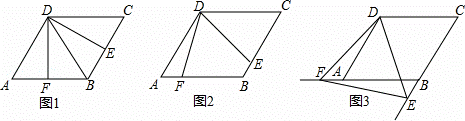
如图,四边形ABCD是边长为2,一个锐角等于60°的菱形纸片,小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合,按顺时针方向旋转三角形纸片,使它的两边分别交CB、BA(或它们的延长线)于点E、F,∠EDF=60°,当CE=AF时,如图1小芳同学得出的结论是DE=DF.
(1)继续旋转三角形纸片,当CE≠AF时,如图2小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由;
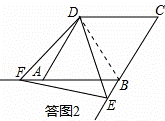
(2)再次旋转三角形纸片,当点E、F分别在CB、BA的延长线上时,如图3请直接写出DE与DF的数量关系;
(3)连EF,若△DEF的面积为y,CE=x,求y与x的关系式,并指出当x为何值时,y有最小值,最小值是多少?
解:(1)DF=DE.理由如下:
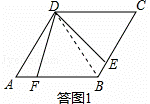
如答图1,连接BD.
∵四边形ABCD是菱形,
∴AD=AB.
又∵∠A=60°,
∴△ABD是等边三角形,
∴AD=BD,∠ADB=60°,
∴∠DBE=∠A=60°
∵∠EDF=60°,
∴∠ADF=∠BDE.∵在△ADF与△BDE中,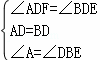 ,
,
∴△ADF≌△BDE(ASA),
∴DF=DE;
(2)DF=DE.理由如下:
如答图2,连接BD.∵四边形ABCD是菱形,
∴AD=AB.
又∵∠A=60°,
∴△ABD是等边三角形,
∴AD=BD,∠ADB=60°,
∴∠DBE=∠A=60°
∵∠EDF=60°,
∴∠ADF=∠BDE.
∵在△ADF与△BDE中,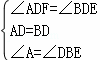 ,
,
∴△ADF≌△BDE(ASA),
∴DF=DE;
(3)由(2)知,△ADF≌△BDE.则S△ADF=S△BDE,AF=BE=x.
依题意得:y=S△BEF+S△ABD=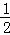 (2+x)xsin60°+
(2+x)xsin60°+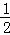 ×2×2sin60°=
×2×2sin60°=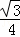 (x+1)2+
(x+1)2+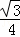 .即y=
.即y=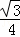 (x+1)2+
(x+1)2+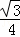 .
.
∵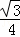 >0,
>0,
∴该抛物线的开口方向向上,
∴当x=0即点E、B重合时,y最小值=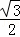 .
.


科目:初中数学 来源: 题型:
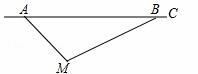
根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为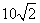 米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到
米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到 B点所用的时间为3秒.
B点所用的时间为3秒.
(1)求测速点M到该公路的距离;
(2)通过计算判断此车是否超速.(参考数据: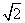 ≈1.41,
≈1.41,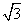 ≈1.73,
≈1.73,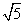 ≈2.24)
≈2.24)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在一个18米高的楼顶上有一信号塔DC,李明同学为了测量信号塔的高度,在地面的A处测的信号塔下端D的仰角为30°,然后他正对塔的方向前进了18米到达地面的B处,又测得信号塔顶端C的仰角为60°,CD⊥AB与点E,E、B、A在一条直线上.请你帮李明同学计算出信号塔CD的高度(结果保留整数,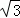 ≈1.7,
≈1.7,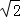 ≈1.4 )
≈1.4 )
查看答案和解析>>
科目:初中数学 来源: 题型:
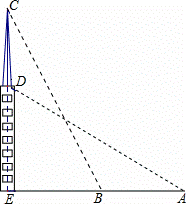
如图,在平面直角坐标系中,等腰△OBC的边OB在x轴上,OB=CB,OB边上的高CA与OC边上的高BE相交于点D,连接OD,AB=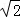 ,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是 .
,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com