
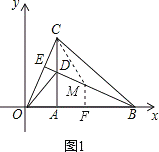
如图,在平面直角坐标系中,等腰△OBC的边OB在x轴上,OB=CB,OB边上的高CA与OC边上的高BE相交于点D,连接OD,AB=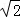 ,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是 .
,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是 .

(1,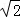 ﹣1)或(﹣
﹣1)或(﹣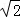 ,
,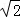 ): 解:∵OB=CB,OB边上的高CA与OC边上的高BE相交于点D,AB=
): 解:∵OB=CB,OB边上的高CA与OC边上的高BE相交于点D,AB=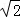 ,∠CBO=45°,
,∠CBO=45°,
∴AB=AC=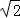 ,OD=CD,
,OD=CD,
在Rt△BAC中,BC=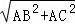 =2,
=2,
∴OB=2,
∴OA=OB﹣AB=2﹣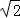 ,
,
在Rt△OAC中,OC=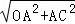 =2
=2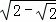 ,
,
在Rt△OAD中,OA2+AD2=OD2,
(2﹣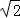 )2+AD2=(
)2+AD2=(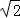 ﹣AD)2,
﹣AD)2,
解得AD=2﹣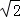 ,
,
∴OD=CD=2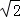 ﹣2,
﹣2,
在Rt△BAD中,BD=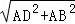 =2
=2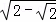 ,
,
①如图1,△BMC∽△CDO时,过M点作MF⊥AB于F,
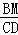 =
=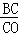 ,即
,即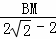 =
=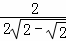 ,
,
解得BM=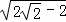 ,
,
∵MF⊥AB,CA是OB边上的高,
∴MF∥DA,
∴△BMF∽△BDA,
∴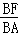 =
=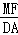 =
=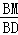 ,即
,即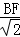 =
= =
=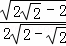 ,
,
解得BF=1,MF=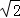 ﹣1,
﹣1,
∴OF=OB﹣BF=1,
∴点M的坐标是(1,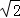 ﹣1);
﹣1);
②如图2,△BCM∽△CDO时,过M点作MF⊥AB于F,
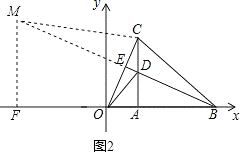
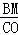 =
=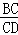 ,即
,即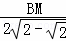 =
=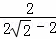 ,
,
解得BM=2 ,
,
∵MF⊥AB,CA是OB边上的高,
∴MF∥DA,
∴△BMF∽△BDA,
∴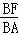 =
=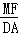 =
=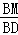 ,即
,即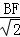 =
=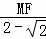 =
=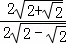 ,
,
解得BF=2+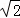 ,MF=
,MF=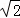 ,
,
∴OF=BF﹣OB=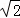 ,
,
∴点M的坐标是(﹣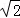 ,
,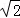 ).
).
综上所述,点M的坐标是(1,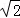 ﹣1)或(﹣
﹣1)或(﹣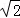 ,
,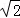 ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
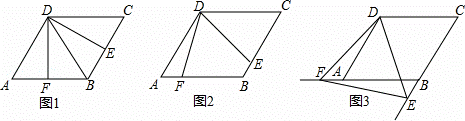
如图,四边形ABCD是边长为2,一个锐角等于60°的菱形纸片,小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合,按顺时针方向旋转三角形纸片,使它的两边分别交CB、BA(或它们的延长线)于点E、F,∠EDF=60°,当CE=AF时,如图1小芳同学得出的结论是DE=DF.
(1)继续旋转三角形纸片,当CE≠AF时,如图2小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由;
(2)再次旋转三角形纸片,当点E、F分别在CB、BA的延长线上时,如图3请直接写出DE与DF的数量关系;
(3)连EF,若△DEF的面积为y,CE=x,求y与x的关系式,并指出当x为何值时,y有最小值,最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
有大小两种货车,2辆大货车与3辆小货车一次可以运货15.5吨,5辆大货车与6辆小货车一次可以运货35吨.设一辆大货车一次可以运货x吨,一辆小货车一次可以运货y吨,根据题意所列方程组正确的是( )
|
| A. |
| B. |
|
|
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
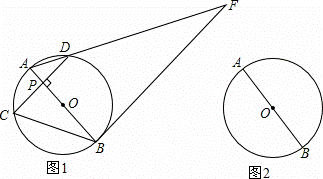
如图1,AB为⊙O的直径,点P是直径AB上任意一点,过点 P作弦CD⊥AB,垂足为P,过点B的直线与线段AD的延长线交于点F,且∠F=∠ABC.
P作弦CD⊥AB,垂足为P,过点B的直线与线段AD的延长线交于点F,且∠F=∠ABC.
(1)若CD=2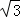 ,BP=4,求⊙O的半径;
,BP=4,求⊙O的半径;
(2)求证:直线BF是⊙O的切线;
(3)当点P与点O重合时,过点A作⊙O的切线交线段BC的延长线于点E,在其它条件不变的情况下,判断四边形AEBF是什么特殊的四边形?请在图2中补全图象并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
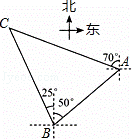
如图,小岛A在港口B的北偏东50°方向,小岛C在港口B的北偏西25°方向,一艘轮船以每小时20海里的速度从港口B出发向小岛A航行,经过5小时到达小岛A,这时测得小岛C在小岛A的北偏西70°方向,求小岛A距离小岛C有多少海里?(最后结果精确到1海里, 参考数据:
参考数据: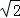 ≈1.1414,
≈1.1414,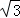 ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com