
����Ŀ��[�Ķ�����]
���조ƽ�а����͡�ȫ��������ģ����֤���߶���ȵ�һ�ַ��������dz������ַ���֤���߶ε��е����⣮
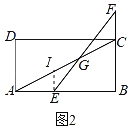
���磺��ͼ��D�ǡ�ABC��AB��һ�㣬E��AC���е㣬����C��CF��AB����DE���ӳ����ڵ�F������֤E���߶�DF���е㣮
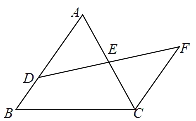
[��������]
�����������Ķ������������۵ľ���ͷ�������������⣮
��1����ͼ1����������ABCD�У���E��AB�ϣ���F��BC���ӳ����ϣ�������AE��CF������EF��AC�ڵ�G��
��֤����G��EF���е㣻
��CG��![]() BE��
BE��
[��չ����]
��2����ͼ2���ھ���ABCD�У�AB��2BC����E��AB�ϣ���F��BC���ӳ����ϣ�������AE��2CF������EF��AC�ڵ�G��̽��BE��CG֮���������ϵ����˵�����ɣ�
��3����ͼ3������E��BA���ӳ����ϣ���F���߶�BC�ϣ�DF��AC�ڵ�H��BF��2��CF��1���� 2���е������������䣬��ֱ��д��GH�ij���
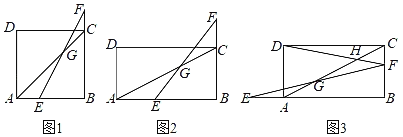
���𰸡���1��������������������������2��BE��![]() CG�����������������3��
CG�����������������3��![]() ��
��
��������
��1���ٹ���E��EI��BC��AC�ڵ�I��֤����EIG�ա�FCG��ASA�����ó�EG��FG���ɣ�
���ɵ���ֱ�������ε����ʵó� AI��![]() AE����ƽ���ߵó�
AE����ƽ���ߵó�![]() ��
��![]() ��
��![]() ��֤��IC��
��֤��IC��![]() BE����ȫ�������ε����ʵó�IG��CG��
BE����ȫ�������ε����ʵó�IG��CG��![]() IC�����ɵó����ۣ�
IC�����ɵó����ۣ�
��2����EI��BC ��AC�ڵ�I�������Ǻ���֤��AE��2IE���ó�IE��CF��֤��EIG�ա�FCG��ASA�����ó�EG��FG��IG��CG����IE��a����AE��2a�����![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ���ó�IC��
���ó�IC��![]() EB�����ɵó������
EB�����ɵó������
��3����FP��AB��AC��P����FP��CD����CFP����ABC��90������CPF����CAB����tan��CPF��![]() ��tan��CAB��
��tan��CAB��![]() ��
��![]() �����AE��PF��2��BC��3��CD��AB��2BC��6��AC��3
�����AE��PF��2��BC��3��CD��AB��2BC��6��AC��3![]() ��֤����CPF�ס�CAB���ó�
��֤����CPF�ס�CAB���ó�![]() ��
��![]() ��
��![]() �����PC��
�����PC��![]() AC��
AC��![]() ��PA��2
��PA��2![]() ��AG��PG��
��AG��PG��![]() ����֤����PFH�ס�CDH���ó�
����֤����PFH�ס�CDH���ó�![]() ��
��![]() ��
��![]() ���ó�PH��
���ó�PH��![]() PC��
PC��![]() �����ɵó������
�����ɵó������
��1��֤����������E��EI��BC��AC�ڵ�I����ͼ1��ʾ��
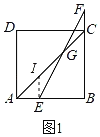
���ı���ABCD�������Σ�
��AB��BC����AEI����ABC��90�㣬
���BAC��45�㣬
���AIE����BAC��45�㣬
��AE��EI��
��AE��CF��
��CF��EI��
��EI��BC��
���EIG����FCG����IEG����CFG��
�ڡ�EIG�͡�FCG�У�
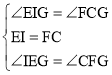 ��
��
���EIG�ա�FCG��ASA����
��EG��FG��
��G��EF���е㣻
����Rt��AEI�У���AEI��90�㣬AE��EI��
���AEI�ǵ���ֱ�������Σ�
��AI��![]() AE��
AE��
��![]() ��
��![]() ��
��
��EI��BC��
��![]() ��
��![]() ��
��![]() ��
��
��IC��![]() BE��
BE��
�ߡ�EIG�ա�FCG��
��IG��CG��![]() IC��
IC��
��CG��![]() ��
��![]() BE��
BE��![]() BE��
BE��
��2���⣺BE��CG֮���������ϵΪ��BE��![]() CG���������£�
CG���������£�
����E��EI��BC ��AC�ڵ�I����ͼ2��ʾ��
���ı���ABCD�Ǿ��Σ�
���AEI����ABC��90�㣬AB��CD��AB��CD��
��Rt��AEI��Rt��ABC�У���ABC����AEI��90�㣬AB��2BC��
��tan��IAE��![]() ��
��![]() ��
��![]() ��
��
��AE��2IE��
��AE��2CF��
��IE��CF��
��EI��BC��
���EIG����FCG����IEG����CFG��
�ڡ�EIG�͡�FCG�У�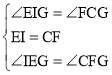 ��
��
���EIG�ա�FCG��ASA����
��EG��FG��IG��CG��
��IE��a����AE��2a��
��Rt��AEI�У���AEI��90�㣬
��AI��![]() ��
��![]() ��
��![]() a��cos��IAE��
a��cos��IAE��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
��EI��BC��
��![]() ��
��![]() ��
��![]() ��
��
��IC��![]() EB��
EB��
��IG��CG��![]() IC��
IC��
��CG��![]() BE��
BE��
��BE��![]() CG��
CG��
��3���⣺��FP��AB��AC��P����ͼ3��ʾ��
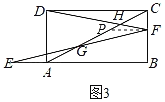
��FP��CD����CFP����ABC��90�㣬��CPF����CAB��
��Rt��CFP��Rt��ABC��AB��2BC��
��tan��CPF��![]() ��tan��CAB��
��tan��CAB��![]() ��
��![]() ��
��
��PF��2CF��
��AE��2CF��
��AE��PF��2��
ͬ��2���ã���AEG�ա�PFG��AAS����
��AG��PG��
��BF��2��CF��1��
��BC��3��CD��AB��2BC��6��
��AC��![]() ��
��![]() ��3
��3![]() ��
��
��FP��AB��
���CPF�ס�CAB��
��![]() ��
��![]() ��
��![]() ��
��
��PC��![]() AC��
AC��![]() ��PA��AC��PC��2
��PA��AC��PC��2![]() ��
��
��AG��PG��![]() PA��
PA��![]() ��
��
��FP��CD��
���PFH�ס�CDH��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��PH��![]() PC��
PC��![]() ��
��
��GH��PG+PH��![]() ��
��![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣨��
���㣨��![]() �ڵ�
�ڵ�![]() ����ࣩ����
����ࣩ����![]() �ύ�ڵ�
�ύ�ڵ�![]() ���Գ�����
���Գ�����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ����������.
����������.
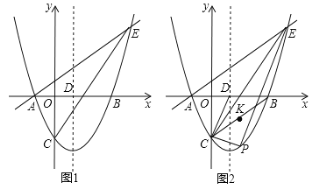
��1����ֱ��![]() �Ľ���ʽ.
�Ľ���ʽ.
��2����![]() Ϊֱ��
Ϊֱ��![]() �·��������ϵ�һ�㣬����
�·��������ϵ�һ�㣬����![]() ��
��![]() .��
.��![]() ��������ʱ������
��������ʱ������![]() ��
��![]() ����
����![]() ���߶�
���߶�![]() ���е㣬��
���е㣬��![]() ���߶�
���߶�![]() �ϵ�һ�㣬��
�ϵ�һ�㣬��![]() ���߶�
���߶�![]() �ϵ�һ�㣬��
�ϵ�һ�㣬��![]() ����Сֵ.
����Сֵ.
��3����![]() ���߶�
���߶�![]() ���е㣬��������
���е㣬��������![]() ��
��![]() ��������ƽ�Ƶõ���������
��������ƽ�Ƶõ���������![]() ��
��![]() ������
������![]() ��
��![]() �Ķ���Ϊ��
�Ķ���Ϊ��![]() ������������
������������![]() �ĶԳ����ϣ��Ƿ���ڵ�
�ĶԳ����ϣ��Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() Ϊ����������?�����ڣ�ֱ��д����
Ϊ����������?�����ڣ�ֱ��д����![]() �����ꣻ�������ڣ���˵������.
�����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����![]() ��
��![]() �ڷ���������ͼ���ϣ���ֱ��
�ڷ���������ͼ���ϣ���ֱ��![]() ������
������![]() ��
��![]() ��
��
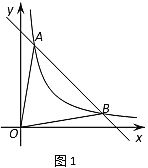
��1�����������ı���ʽ��![]() ��ֵ��
��ֵ��
��2����![]() �������
�������
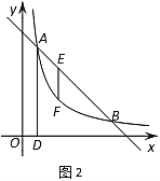
��3����ͼ2��![]() ���߶�
���߶�![]() ��һ�㣬��
��һ�㣬��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ��Ĵ��ߣ�������������ͼ���ڵ�
��Ĵ��ߣ�������������ͼ���ڵ�![]() ����
����![]() �������
�������![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() Ϊ
Ϊ![]() ��ֱ����
��ֱ����![]() Ϊ
Ϊ![]() �����ߣ�
�����ߣ�![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��![]() ��
Ϊ��![]() ���е㣬����
���е㣬����![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��
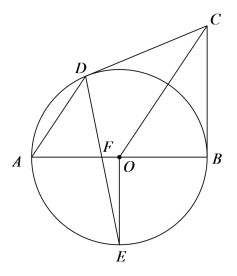
(1)��֤��![]() Ϊ
Ϊ![]() �����ߣ�
�����ߣ�
(2)��֤��![]() ��
��
(3)��![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���������У���ӣ�ȷ��ʦ��������ȫ�����彡����������2020��1��29���·�֪ͨ��Ҫ����괺��ѧ�����ڿ�ѧ����ͣ�β�ͣѧ����ͳ���������������Դ���н�ѧ��ijУΪ����ѧ���ܹ��ﵽ��ѵ�ѧϰЧ����ȷ����ʦ�ǿ���ѡ����������ֱ���ڿη�ʽ��A���ǻ���ֱ����B������ֱ����C����Ѷ����ֱ����
��1��������ʦ�����������ڿη�ʽ�����ѡȡһ�֣����ǻ���ֱ���ĸ���Ϊ�� ����
��2�������������λ��ʦ���������ѡȡһ������ֱ����ʽ�����ڿΣ��������б�������״ͼ������������������λ��ʦѡȡ��ͬ������ֱ���ڿη�ʽ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
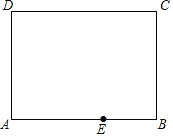
����Ŀ����ͼ��һ�ž���ֽƬABCD����֪AB��8��AD��6��EΪAB��һ�㣬AE��5����Ҫ����һ�ŵ���������ֽƬ����AEP����ʹ��P���ھ���ABCD��ijһ�����ϣ������������AEP�ĵױ��ϵĸߵij���_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
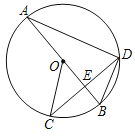
����Ŀ����ͼ����![]() �У�
�У�![]() ��ֱ����
��ֱ����![]() ���ң�
���ң�![]() ������Ϊ
������Ϊ![]() ������
������![]() ��
��![]() ��
��![]() ��������˵������ȷ���ǣ� ��
��������˵������ȷ���ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�����о�������![]() ��
��![]() Ϊ������ʱ���õ����½��ۣ�������ȷ���ǣ� ��
Ϊ������ʱ���õ����½��ۣ�������ȷ���ǣ� ��
A.����![]() ȡ��ʵ����
ȡ��ʵ����![]() ��ֵ��С��0
��ֵ��С��0
B.�������ߵĶ���ʼ����ֱ��![]() ��
��
C.��![]() ʱ��
ʱ��![]() ��
��![]() �������������
�������������![]()
D.����������������![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̨�ؽ�����������Ϊ���������ү������ƶ�����������������ү�Լ��ֹ�������������ɱ�Ϊÿ��40Ԫ�����ۼ�Ϊÿ��80Ԫʱ��ÿ�¿�����100��.Ϊ����������˿ͣ���ȡ���۴�ʩ.���г����鷴ӳ�����۵���ÿ��1Ԫ����ÿ�¿ɶ�����5��.��ÿ���������ۼ�Ϊ![]() Ԫ��
Ԫ��![]() Ϊ����������ÿ�µ�������Ϊ
Ϊ����������ÿ�µ�������Ϊ![]() ����
����
��1��ֱ��д��![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2���������ÿ�»�õ�����Ϊ![]() Ԫ�������۵��۽��Ͷ���Ԫʱ��ÿ�»�õ����������������Ƕ��٣�
Ԫ�������۵��۽��Ͷ���Ԫʱ��ÿ�»�õ����������������Ƕ��٣�
��3�����ү��з�ƶ���߸��Լ������ĺô���Ϊ�˻ر���ᣬ������ÿ�´������о��200Ԫ����ƶ��ѧ��.Ϊ�˱�֤����ÿ��������4220Ԫ�������۵���Ӧ�ö���ʲô��Χ�ڣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com