
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 为
为![]() 的切线,
的切线,![]() ,交
,交![]() 于点
于点![]() ,
,![]() 为弧
为弧![]() 的中点,连接
的中点,连接![]() ,交
,交![]() 于点
于点![]() .
.
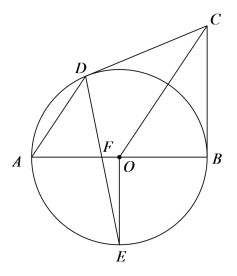
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() ,求
,求![]() .
.
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)连接OD,根据平行线的性质和等腰三角形的性质,得出相等的边和角,然后判断出△CDO≌△CBO,判断出∠CDO是直角即可解决.
(2)根据圆周角定理的推论,判断出∠ADB为90°,再结合平行线的性质得出相等的角,根据相似三角形的判定方法证明△ABD∽△OCB,然后根据相似三角形的性质列出比例式,将比例式变形即可解决.
(3)过点D向AB作垂线,设![]() ,根据射影定理,得出AG的长度,计算出OG的长度,根据勾股定理计算出DG的长度,由垂径定理得出∠AOE的度数,然后结合平行线的性质得出相似三角形,列出比例式,即可解决.
,根据射影定理,得出AG的长度,计算出OG的长度,根据勾股定理计算出DG的长度,由垂径定理得出∠AOE的度数,然后结合平行线的性质得出相似三角形,列出比例式,即可解决.
(1)连接![]() ,
,
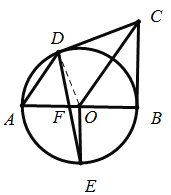
![]() 为⊙
为⊙![]() 的切线,
的切线,![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
即![]() .
.
![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)连接![]() ,
,
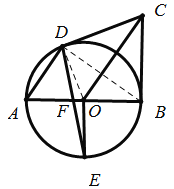
![]() 为⊙
为⊙![]() 的直径,
的直径,
![]() .
.
又![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
又∵AB=2OB=2OA,OA=OB,
∴![]() ;
;
(3)作![]() ,垂足为
,垂足为![]() ,设
,设![]() .
.
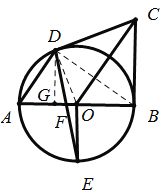
![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
 .
.
![]() 为
为![]() 的中点,
的中点,
![]() ,
,
![]() .
.
![]() ,
,
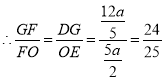 .
.
![]() .
.
 .
.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
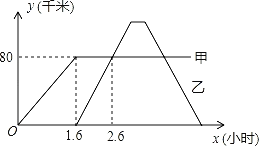
【题目】A,B两地相距200千米.早上8:00货车甲从A地出发将一批物资运往B地,行驶一段路程后出现故障,即刻停车与B地联系.B地收到消息后立即派货车乙从B地出发去接运甲车上的物资.货车乙遇到甲后,用了18分钟将物资从货车甲搬运到货车乙上,随后开往B地.两辆货车离开各自出发地的路程y(千米)与时间x(小时)的函数关系如图所示.(通话等其他时间忽略不计)
(1)求货车乙在遇到货车甲前,它离开出发地的路程y关于x的函数表达式.
(2)因实际需要,要求货车乙到达B地的时间比货车甲按原来的速度正常到达B地的时间最多晚1个小时,问货车乙返回B地的速度至少为每小时多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
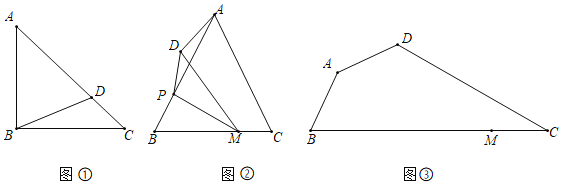
(1)如图①,在等腰Rt△ABC中,斜边AC=4,点D为AC上一点,连接BD,则BD的最小值为 ;
问题探究
(2)如图②,在△ABC中,AB=AC=5,BC=6,点M是BC上一点,且BM=4,点P是边AB上一动点,连接PM,将△BPM沿PM翻折得到△DPM,点D与点B对应,连接AD,求AD的最小值;
问题解决
(3)如图③,四边形ABCD是规划中的休闲广场示意图,其中∠BAD=∠ADC=135°,∠DCB=30°,AD=2![]() km,AB=3km,点M是BC上一点,MC=4km.现计划在四边形ABCD内选取一点P,把△DCP建成商业活动区,其余部分建成景观绿化区.为方便进入商业区,需修建小路BP、MP,从实用和美观的角度,要求满足∠PMB=∠ABP,且景观绿化区面积足够大,即△DCP区域面积尽可能小.则在四边形ABCD内是否存在这样的点P?若存在,请求出△DCP面积的最小值;若不存在,请说明理由.
km,AB=3km,点M是BC上一点,MC=4km.现计划在四边形ABCD内选取一点P,把△DCP建成商业活动区,其余部分建成景观绿化区.为方便进入商业区,需修建小路BP、MP,从实用和美观的角度,要求满足∠PMB=∠ABP,且景观绿化区面积足够大,即△DCP区域面积尽可能小.则在四边形ABCD内是否存在这样的点P?若存在,请求出△DCP面积的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△OA1B1,顶点A1在双曲线y=![]() (x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2,过A2作A2B2∥A1B1交x轴于点B2,得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3,过A3作A3B3∥A2B2交x轴于点B3,得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为_____.
(x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2,过A2作A2B2∥A1B1交x轴于点B2,得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3,过A3作A3B3∥A2B2交x轴于点B3,得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
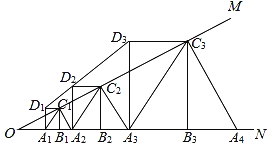
【题目】如图,∠MON=30°,点A1在ON上,点C1在OM上,OA1=A1C1=2,C1B1⊥ON于点B1,以A1B1和B1C1为邻边作矩形A1B1C1D1,点A1,A2关于点B对称,A2C2∥A1C1交OM于点C2,C2B2⊥ON于点B2,以A2B2和B2C2为邻边作矩形A2B2C2D2,连接D1D2,点A2,A3关于点B2对称,A3C3∥A2C2交OM于点C3,C3B3⊥ON于点B3,以A3B3和B3C3为邻边作矩形A3B3C3D3,连接D2D3,……依此规律继续下去,则DnDn+1=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[阅读理解]
构造“平行八字型”全等三角形模型是证明线段相等的一种方法,我们常用这种方法证明线段的中点问题.
例如:如图,D是△ABC边AB上一点,E是AC的中点,过点C作CF∥AB,交DE的延长线于点F,则易证E是线段DF的中点.
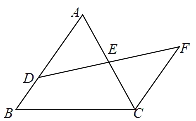
[经验运用]
请运用上述阅读材料中所积累的经验和方法解决下列问题.
(1)如图1,在正方形ABCD中,点E在AB上,点F在BC的延长线上,且满足AE=CF,连接EF交AC于点G.
求证:①G是EF的中点;
②CG=![]() BE;
BE;
[拓展延伸]
(2)如图2,在矩形ABCD中,AB=2BC,点E在AB上,点F在BC的延长线上,且满足AE=2CF,连接EF交AC于点G.探究BE和CG之间的数量关系,并说明理由;
(3)如图3,若点E在BA的延长线上,点F在线段BC上,DF交AC于点H,BF=2,CF=1,( 2)中的其它条件不变,请直接写出GH的长.
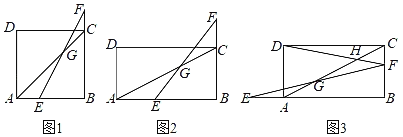
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,楼房BD的前方竖立着旗杆AC.小亮在B处观察旗杆顶端C的仰角为45°,在D处观察旗杆顶端C的俯角为30°,楼高BD为20米.
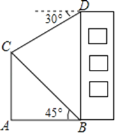
(1)求∠BCD的度数;
(2)求旗杆AC的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区计划对面积为3600m2的区域进行绿化,经投标,由甲,乙两个工程队来完成,已知甲队4天能完成绿化的面积等于乙队8天完成绿化的面积,甲队3天能完成绿化的面积比乙队5天能完成绿化面积多50m2
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)若甲队每天化费用是1.2万元,乙队每天绿化费用为0.5万元,要使这次绿化的总费用不超过40万元,则至少应安排乙工程队绿化多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com