
【题目】观察下列等式:
①sin30°=![]() ,cos60°=
,cos60°=![]() ;
;
②sin45°=![]() ,cos45°=
,cos45°=![]() ;
;
③sin60°=![]() ,cos30°=
,cos30°=![]() .
.
(1)根据上述规律,计算sin2α+sin2(90°-α)= .
(2)计算:sin21°+sin22°+sin23°+…+sin289°.
【答案】(1)1(2)![]()
【解析】分析:
(1)观察、分析所给等式可得:![]() ,结合
,结合![]() 即可求得本题的答案为1;
即可求得本题的答案为1;
(2)把原式化为(sin21°+sin289)+(sin22°+sin288°)+…+sin245°,再结合(1)中所得结论进行计算即可求得本题答案.
详解:
(1)∵根据已知的式子可以得到sin(90°-α)=cosα,
∴sin2α+sin2(90°-α)= sin2α+cos2α=1;
(2)由(1)中结论可得:
sin21°+sin22°+sin23°+…+sin289°
=(sin21°+sin289)+(sin22°+sin288°)+…+sin245°
=1+1+…1+![]()
=44+![]()
=![]() .
.


科目:初中数学 来源: 题型:
【题目】某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前6名选手的得分如下:
序号 项目 | 1 | 2 | 3 | 4 | 5 | 6 |
笔试成绩/分 | 85 | 92 | 84 | 90 | 84 | 80 |
面试成绩/分 | 90 | 88 | 86 | 90 | 80 | 85 |
根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为100分).
(1)这6名选手笔试成绩的中位数是________分,众数是________分;
(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(3)求出其余五名选手的综合成绩,并以综合成绩排序确定前两名人选.
查看答案和解析>>
科目:初中数学 来源: 题型:
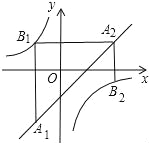
【题目】如图,已知点A1,A2,…,An均在直线y=x﹣1上,点B1,B2,…,Bn均在双曲线y=﹣![]() 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=﹣1,则a2016= .
上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=﹣1,则a2016= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知一个正分数![]() (m>n>0),将分子、分母同时增加1,得到另一个正分数
(m>n>0),将分子、分母同时增加1,得到另一个正分数![]() ,比较
,比较![]() 和
和![]() 的值的大小,并证明你的结论;
的值的大小,并证明你的结论;
(2)若正分数![]() (m>n>0)中分子和分母同时增加k(整数k>0),则
(m>n>0)中分子和分母同时增加k(整数k>0),则![]() _____
_____![]() .
.
(3)请你用上面的结论解释下面的问题:
建筑学规定:民用住宅窗户面积必须小于地板面积,但按采光标准,窗户面积与地板面积的比应不小于10%,并且这个比值越大,住宅的采光条件越好.若原来的地板面积和窗户面积分别为x,y,同时增加相等的窗户面积和地板面积,则住宅的采光条件是变好还是变坏?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
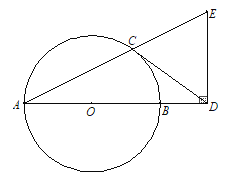
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若tan∠CAB=![]() ,AB=3,求BD的长.
,AB=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC=______度;
(2)求∠EDF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在数轴上有三点![]() ,
,![]() ,
,![]() ,点
,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,且
,且![]() 、
、![]() 满足
满足![]() .沿
.沿![]() ,
,![]() ,
,![]() 三点中的一点折叠数轴,若另外两点互相重合,则点
三点中的一点折叠数轴,若另外两点互相重合,则点![]() 表示的数是________.
表示的数是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
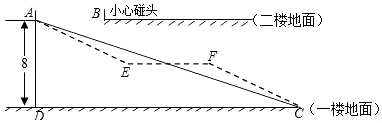
【题目】某大型购物商场在一楼和二楼之间安装自动扶梯AC,截面如图所示,一楼和二楼地面平行(即AB所在的直线与CD平行),层高AD为8米,∠ACD=20°,为使得顾客乘坐自动扶梯时不至于碰头,A、B之间必须达到一定的距离.
(1)要使身高2.26米的姚明乘坐自动扶梯时不碰头,那么A、B之间的距离至少要多少米?(精确到0.1米)
(2)如果自动扶梯改为由AE、EF、FC三段组成(如图中虚线所示),中间段EF为平台(即EF∥DC),AE段和FC段的坡度i=1:2,求平台EF的长度.(精确到0.1米)
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
查看答案和解析>>
科目:初中数学 来源: 题型:
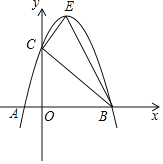
【题目】如图,已知抛物线![]() 经过点
经过点![]() 和点
和点![]() ,点C为抛物线与y轴的交点.
,点C为抛物线与y轴的交点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若点E为直线BC上方抛物线上的一点,请求出
若点E为直线BC上方抛物线上的一点,请求出![]() 面积的最大值.
面积的最大值.
![]() 在
在![]() 条件下,是否存在这样的点
条件下,是否存在这样的点![]() ,使得
,使得![]() 为等腰三角形?如果有,请直接写出点D的坐标;如果没有,请说明理由.
为等腰三角形?如果有,请直接写出点D的坐标;如果没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com