
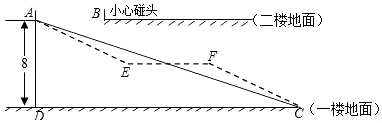
【题目】某大型购物商场在一楼和二楼之间安装自动扶梯AC,截面如图所示,一楼和二楼地面平行(即AB所在的直线与CD平行),层高AD为8米,∠ACD=20°,为使得顾客乘坐自动扶梯时不至于碰头,A、B之间必须达到一定的距离.
(1)要使身高2.26米的姚明乘坐自动扶梯时不碰头,那么A、B之间的距离至少要多少米?(精确到0.1米)
(2)如果自动扶梯改为由AE、EF、FC三段组成(如图中虚线所示),中间段EF为平台(即EF∥DC),AE段和FC段的坡度i=1:2,求平台EF的长度.(精确到0.1米)
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
【答案】(1)6.3;(2)6.2
【解析】
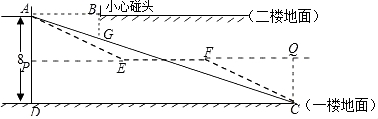
试题分析:(1)连接AB,作BG⊥AB交AC于点G,在Rt△ABG中,利用已知条件求出AB的长即可;
(2)设直线EF交AD于点P,作CQ⊥EF于点Q,设AP=x,则PE=2x,PD=8﹣x,在Rt△ACD中利用已知数据可求出CD的长,进而可求出台EF的长度.
试题解析:(1)连接AB,作BG⊥AB交AC于点G,则∠ABG=90°
∵AB∥CD,∴∠BAG=∠ACD=20°,
在Rt△ABG中,![]() ,
,
∵BG=2.26,tan20°≈0.36,
∴![]() ,
,
∴AB≈6.3,
答:A、B之间的距离至少要6.3米.
(2)设直线EF交AD于点P,作CQ⊥EF于点Q,
∵AE和FC的坡度为1:2,
∴![]() ,
,
设AP=x,则PE=2x,PD=8﹣x,
∵EF∥DC,
∴CQ=PD=8﹣x,
∴FQ=2(8﹣x)=16﹣2x,
在Rt△ACD中,![]() ,
,
∵AD=8,∠ACD=20°,
∴CD≈22.22
∵PE+EF+FQ=CD,
∴2x+EF+16﹣2x=22.22,
∴EF=6.22≈6.2
答:平台EF的长度约为6.2米.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
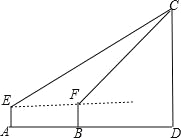
【题目】如图,一游客在某城市旅游期间,沿街步行前往著名的电视塔观光,他在A处望塔顶C的仰角为30°,继续前行250m后到达B处,此时望塔顶的仰角为45°.已知这位游客的眼睛到地面的距离约为170cm,假若游客所走路线直达电视塔底.请你计算这座电视塔大约有多高?(结果保留整数. ![]() ≈1.7,
≈1.7,![]() ≈1.4;E,F分别是两次测量时游客眼睛所在的位置.)
≈1.4;E,F分别是两次测量时游客眼睛所在的位置.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级(2)班50名学生进行一分钟跳绳测试,将所得数据整理后,得到落在180次~189次区间的百分比为28%,则在180次~189次区间的人数是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合运用:
(1)已知![]() ,求a2+
,求a2+![]() 的值.
的值.
(2)已知a是4+![]() 的小数部分,b是﹣
的小数部分,b是﹣![]() +5的小数部分,c是(﹣
+5的小数部分,c是(﹣![]() +2)﹣1的整数部分,求a2c﹣b2c的值.
+2)﹣1的整数部分,求a2c﹣b2c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某山区有23名中小学生因贫困失学需要捐助,资助一名中学生需要学习费用a元,资助一名小学生需要学习费用b元,某校学生积极捐款,初中各年级学生捐款数额与用其恰好能帮助的贫困中学生和小学生人数的部分情况如下表:
七年级 | 八年级 | 九年级 | |
捐款数额(元) | 4000 | 4200 | 7400 |
捐助贫困中学生(名) | 2 | 3 | |
捐助贫困小学生(名) | 4 | 3 |
(1)求a、b的值;
(2)九年级学生的捐款解决了其余贫困中小学生的学习费用,请将九年级学生可捐助的贫困中、小学生人数直接填入上表中(不需要写出计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校学生的每日运动量,收集数据正确的是( )
A.调查该校舞蹈队学生每日的运动量
B.调查该校书法小组学生每日的运动量
C.调查该校田径队学生每日的运动量
D.调查该校某一班级的学生每日的运动量
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com