
【题目】如图,已知等边△ABC内接于⊙O,点P为![]() 上任意一点(点P不与点A、点B重合),连结PB、PO,取BC的中点D,取OP的中点E,连结DE,若∠OED=α,则∠PBC的度数为_____.(用含α的代数式表示)
上任意一点(点P不与点A、点B重合),连结PB、PO,取BC的中点D,取OP的中点E,连结DE,若∠OED=α,则∠PBC的度数为_____.(用含α的代数式表示)
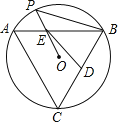
【答案】60°+α.
【解析】
根据圆内接等边三角形的性质表示∠EOD的度数,再根据四边形内角和表示出∠BED的度数,进而根据三角形内角和即可求解.
解:如图:连接OD、OB,
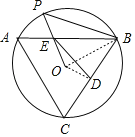
∵等边△ABC内接于⊙O,
∴OD⊥BC,OD=![]() OB,∠OBD=30°.
OB,∠OBD=30°.
∵E点是OP的中点,
∴OE=![]() OP,
OP,
∵OB=OP,
∴OD=OE,
∴∠OED=∠ODE=α,
∴∠EOD=180°﹣2α.
因为四边形DOEB内角和为360°,
∴∠BED=360°﹣90°﹣60°﹣(180﹣2α)﹣α=30°+α,
∠EOB=180°﹣30°﹣(30+2α)=120﹣2α.
∵OB=OP,
∴∠P=∠OBP=![]() (180°﹣∠POB)=
(180°﹣∠POB)=![]() (180﹣120+2α)=30°+α.
(180﹣120+2α)=30°+α.
∴∠PBC=∠OBP+∠OBC=30°+α+30°=60°+α.
故答案为60°+α.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
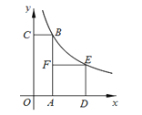
【题目】如图,四边形![]() 是矩形,四边形
是矩形,四边形![]() 是正方形,点
是正方形,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 上,点
上,点![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,![]() ,则正方形
,则正方形![]() 的面积为( )
的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】瑞安市曹村镇“八百年灯会”成为温州“申遗”的宝贵项目.某公司生产了一种纪念花灯,每件纪念花灯制造成本为18元.设销售单价x(元),每日销售量y(件)每日的利润w(元).在试销过程中,每日销售量y(件)、每日的利润w(元)与销售单价x(元)之间存在一定的关系,其几组对应量如下表所示:
(元) | 19 | 20 | 21 | 30 |
(件) | 62 | 60 | 58 | 40 |
(1)根据表中数据的规律,分别写出毎日销售量y(件),每日的利润w(元)关于销售单价x(元)之间的函数表达式.(利润=(销售单价﹣成本单价)×销售件数).
(2)当销售单价为多少元时,公司每日能够获得最大利润?最大利润是多少?
(3)根据物价局规定,这种纪念品的销售单价不得高于32元,如果公司要获得每日不低于350元的利润,那么制造这种纪念花灯每日的最低制造成本需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC边中点.点M为线段BC上的一个动点(不与点C,点D重合),连接AM,将线段AM绕点M顺时针旋转90°,得到线段ME,连接EC.
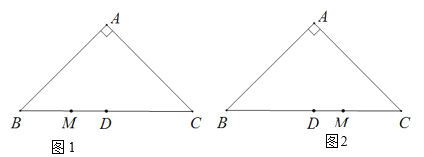
(1)如图1,若点M在线段BD上.
① 依据题意补全图1;
② 求∠MCE的度数.
(2)如图2,若点M在线段CD上,请你补全图形后,直接用等式表示线段AC、CE、CM之间的数量关系 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.
(1)判断BD与圆O的位置关系,并证明你的结论;
(2)当OA=3,OC=1时,求线段BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
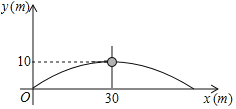
【题目】一球从地面抛出的运动路线呈抛物线,如图.当球离抛出地的水平距离为30m时,达到最大高度10m.
(1)问:球被抛出多远?并求出该抛物线的解析式.
(2)当球的高度为![]() m时,球离抛出地的水平距离是多少?
m时,球离抛出地的水平距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC.则下列结论:①abc>0;②9a+3b+c>0;③c>﹣1;④关于x的方程ax2+bx+c=0(a≠0)有一个根为﹣![]() ;⑤抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<2<x2,且x1+x2>4,则y1>y2.其中正确的结论有( )
;⑤抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<2<x2,且x1+x2>4,则y1>y2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若凸四边形的两条对角线所夹锐角为60°,我们称这样的凸四边形为“美丽四边形”.
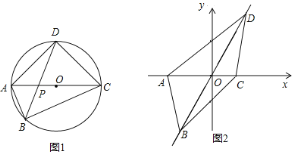
(1)若矩形ABCD是“美丽四边形”,且AB=3,则BC= ;
(2)如图1,“美丽四边形”ABCD内接于⊙O,AC与BD相交于点P,且对角线AC为直径,AP=1,PC=5,求另一条对角线BD的长;
(3)如图2,平面直角坐标系中,已知“美丽四边形”ABCD的四个顶点A(﹣3,0)、C(2,0),B在第三象限,D在第一象限,AC与BD交于点O,且四边形ABCD的面积为![]() ,若二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象同时经过这四个顶点,求a的值.
,若二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象同时经过这四个顶点,求a的值.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com