
【题目】若凸四边形的两条对角线所夹锐角为60°,我们称这样的凸四边形为“美丽四边形”.
(1)若矩形ABCD是“美丽四边形”,且AB=3,则BC= ;
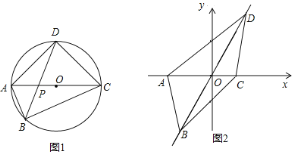
(2)如图1,“美丽四边形”ABCD内接于⊙O,AC与BD相交于点P,且对角线AC为直径,AP=1,PC=5,求另一条对角线BD的长;
(3)如图2,平面直角坐标系中,已知“美丽四边形”ABCD的四个顶点A(﹣3,0)、C(2,0),B在第三象限,D在第一象限,AC与BD交于点O,且四边形ABCD的面积为![]() ,若二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象同时经过这四个顶点,求a的值.
,若二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象同时经过这四个顶点,求a的值.![]()
【答案】(1)3![]() 或
或![]() ;(2)2
;(2)2![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据矩形ABCD对角线相等且互相平分,再加上对角线夹角为60°,即出现等边三角形,所以得到矩形相邻两边的比等于tan60°.由于AB边不确定是较长还是较短的边,故需要分类讨论计算.
(2)过O点作OH垂直BD,连接OD,由∠DPC=60°可求得OH,在Rt△ODH中勾股定理可求DH,再由垂径定理可得BD=2DH.
(3)由BD与x轴成60°角可知直线BD解析为y=![]() x,由二次函数图象与x轴交点为A、C可设解析式为y=a(x+3)(x-2),把两解析式联立方程组,消去y后得到关于x的一元二次方程,解即为点B、D横坐标,所以用韦达定理得到xB+xD和xBxD进而得到用a表示的(xB-xD)2.又由四边形面积可求得xB-xD=6,即得到关于a的方程并解方程求得a.
x,由二次函数图象与x轴交点为A、C可设解析式为y=a(x+3)(x-2),把两解析式联立方程组,消去y后得到关于x的一元二次方程,解即为点B、D横坐标,所以用韦达定理得到xB+xD和xBxD进而得到用a表示的(xB-xD)2.又由四边形面积可求得xB-xD=6,即得到关于a的方程并解方程求得a.
解:(1)设矩形ABCD对角线相交于点O
∴AC=BD,AO=CO,BO=DO,∠ABC=90°
∴AO=BO=CO=DO
∵矩形ABCD是“美丽四边形”∴AC、BD夹角为60°
i)如图,若AB=3为较短的边,则∠AOB=60°
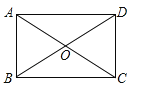
∴△OAB是等边三角形
∴∠OAB=60°∴Rt△ABC中,tan∠OAB=![]() ∴BC=
∴BC=![]() AB=3
AB=3![]()
ii)如图,若AB=3为较长的边,则∠BOC=60°
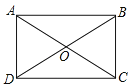
∴△OBC是等边三角形
∴OCB=60°∴Rt△ABC中,tan∠OCB=![]()
∴BC=![]()
故答案为:3![]() 或
或![]() .
.
(2)过点O作OH⊥BD于点H,连接OD

∴∠OHP=∠OHD=90°,BH=DH=![]() BD∵AP=1,PC=5
BD∵AP=1,PC=5
∴⊙O直径AC=AP+PC=6∴OA=OC=OD=3
∴OP=OA﹣AP=3﹣1=2
∵四边形ABCD是“美丽四边形”
∴∠OPH=60°∴Rt△OPH中,sin∠OPH=![]() ∴OH=
∴OH=![]() OP=
OP=![]() ∴Rt△ODH中,DH=
∴Rt△ODH中,DH=![]()
∴BD=2DH=2![]()
(3)过点B作BM⊥x轴于点M,过点D作DN⊥x轴于点N
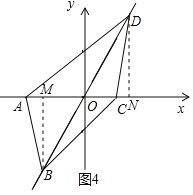
∴∠BMO=∠DNO=90°
∵四边形ABCD是“美丽四边形”∴∠BOM=∠DON=60°
∴tan∠DON=![]() ,即
,即![]()
∴直线BD解析式为y=![]() x
x
∵二次函数的图象过点A(﹣3,0)、C(2,0),即与x轴交点为A、C
∴用交点式设二次函数解析式为y=a(x+3)(x﹣2)
∵ 整理得:ax2+(a﹣
整理得:ax2+(a﹣![]() )x﹣6a=0
)x﹣6a=0
∴xB+xD=﹣![]() ,xBxD=﹣6
,xBxD=﹣6
∴(xB﹣xD)2=(xB+xD)2﹣4xBxD=(﹣![]() )2+24
)2+24
∵S四边形ABCD=S△ABC+S△ACD=![]() ACBM+
ACBM+![]() ACDN=
ACDN=AC(BM+DN)
=![]() AC(yD﹣yB)=
AC(yD﹣yB)=![]() AC(
AC(![]() xD﹣
xD﹣![]() xB)=
xB)=![]() (xB﹣xD)
(xB﹣xD)
∴![]() (xB﹣xD)=15
(xB﹣xD)=15![]()
∴xB﹣xD=6∴(﹣![]() )2+24=36
)2+24=36
解得:a1=![]() ,a2=
,a2=![]()
∴a的值为![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC内接于⊙O,点P为![]() 上任意一点(点P不与点A、点B重合),连结PB、PO,取BC的中点D,取OP的中点E,连结DE,若∠OED=α,则∠PBC的度数为_____.(用含α的代数式表示)
上任意一点(点P不与点A、点B重合),连结PB、PO,取BC的中点D,取OP的中点E,连结DE,若∠OED=α,则∠PBC的度数为_____.(用含α的代数式表示)
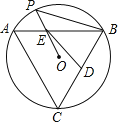
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图,图象过点(﹣1,0),对称轴为直线
的部分图象如图,图象过点(﹣1,0),对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时, ![]() 随
随![]() 的增大而增大.其中正确的结论有( )
的增大而增大.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】. 在一个不透明的布袋中装有三个小球,小球上分别标有数字﹣1、0、2,它们除了数字不同外,其他都完全相同.
(1)随机地从布袋中摸出一个小球,则摸出的球为标有数字2的小球的概率为 ;
(2)小丽先从布袋中随机摸出一个小球,记下数字作为平面直角坐标系内点M的横坐标.再将此球放回、搅匀,然后由小华再从布袋中随机摸出一个小球,记下数字作为平面直角坐标系内点M的纵坐标,请用树状图或表格列出点M所有可能的坐标,并求出点M落在如图所示的正方形网格内(包括边界)的概率.
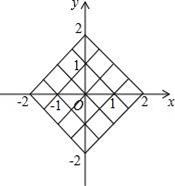
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的![]() 个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这![]() 个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】临近期末考试,心理专家建议考生可通过以下四种方式进行考前减压:![]() .享受美食,
.享受美食,![]() .交流谈心,
.交流谈心,![]() .体育锻炼,
.体育锻炼,![]() .欣赏艺术.
.欣赏艺术.
(1)随机采访一名九年级考生,选择其中某一种方式,他选择“享受美食”的概率是 .
(2)同时采访两名九年级考生,请用画树状图或列表的方法求他们中至少有一人选择“欣赏艺术”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的苹果.经市场调研发现:若每箱以50元的价格销售,平均每天销售90箱;价格每提高1元,则平均每天少销售3箱.设每箱的销售价为x元(x>50),平均每天的销售量为y箱,该批发商平均每天的销售利润w元.
(1)y与x之间的函数解析式为__________;
(2)求w与x之间的函数解析式;
(3)当x为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C,与x轴交于A,B两点,其中点B的坐标为B(4,0),抛物线的对称轴交x轴于点D,CE∥AB,并与抛物线的对称轴交于点E.现有下列结论:①a>0;②b>0;③4a+2b+c<0;④AD+CE=4.其中所有正确结论的序号是( )
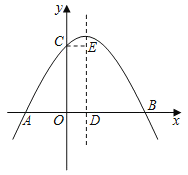
A.①②B.①③C.②③D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com