
【题目】如图,AC平分∠BAD,CD⊥AD,CB⊥AB,连结BD.请找出图中所有的等腰三角形,并说明理由.
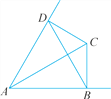
【答案】等腰三角形有△ABD和△BCD
【解析】试题分析:本题先利用角平分线的性质可证CD=CB,再根据HL判定△ADC≌△ADC,根据AC平分∠BAD,CD⊥AD,CB⊥AB,可证CD=CB,所以△CDB是等腰三角形.在Rt△ADC和Rt△ABC中,由CD=CB,AC=AC,可判定Rt△ADC≌Rt△ABC,从而可得AD=AB,所以△ABD是等腰三角形.
试题解析:等腰三角形有△ABD和△BCD,
理由如下:
∵ AC平分∠BAD,CD⊥ AD,CB⊥ AB,
∴ CD=CB,
∴ △CDB是等腰三角形,
在Rt△ADC和Rt△ABC中,
![]() ,
,
∴ Rt△ADC≌Rt△ABC(HL),
∴ AD=AB,
∴ △ ABD是等腰三角形.
点睛:本题要考查角平分线的性质,HL判定定理,等腰三角形的判定,解决本题的关键在于熟练掌握角平分线的性质,利用角平分线上的点到角两边的距离相等证明线段相等,再利用HL进行全等判定.


科目:初中数学 来源: 题型:
【题目】选出下列不具有相反意义的量( )
A. 气温升高4℃与气温12℃ B. 胜3局与负4局
C. 转盘逆时针转4圈与顺时针转6圈 D. 支出5万元与收入3万元
查看答案和解析>>
科目:初中数学 来源: 题型:
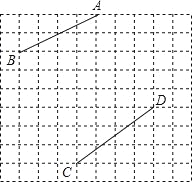
【题目】如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
(1)在方格纸中画以AB为斜边的等腰直角三角形ABE;
(2)在方格纸中画以CD为一边的三角形CDF,点F在小正方形的顶点上,且三角形CDF的面积为5,tan∠DCF=![]() ,连接EF,并直接写出线段EF的长.
,连接EF,并直接写出线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)5+(﹣6)﹣(﹣2)
(2)|﹣4|﹣12×( ![]() ﹣
﹣ ![]() )
)
(3)![]() +(﹣
+(﹣ ![]() )2÷(﹣
)2÷(﹣ ![]() )
)
(4)2×(﹣1)2012+ ![]() ÷(﹣
÷(﹣ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了有效控制酒后驾驶,石家庄市某交警的汽车在一条南北方向的大街上巡逻,规定向北为正,向南为负,已知从出发点开始所行使的路程(单位:千米)为:+3,﹣2,+1,+2,﹣3,﹣1,+2
(1)若此时遇到紧急情况要求这辆汽车回到出发点,请问司机该如何行使?
(2)当该辆汽车回到出发点时,一共行驶了多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com