
 如图,在矩形ABCD中,两条对角线AC与BD相交于点O,AB=6,OA=4,则AD的长为( )
如图,在矩形ABCD中,两条对角线AC与BD相交于点O,AB=6,OA=4,则AD的长为( )| A. | 4 | B. | 8 | C. | 3$\sqrt{3}$ | D. | 2$\sqrt{7}$ |
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 有理数的大小关系如图所示,则下列式子中一定成立的是( )
有理数的大小关系如图所示,则下列式子中一定成立的是( )| A. | a+b+c>0 | B. | |a+b|<c | C. | |a-c|=|a|+c | D. | |b-c|>|c-a| |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠B=90°,分别以点A、C为圆心,大于$\frac{1}{2}$AC长为半径画弧,两弧相交于点M、N,连接MN,与AC、BC分别交于点D、E,连接AE.
如图,在Rt△ABC中,∠B=90°,分别以点A、C为圆心,大于$\frac{1}{2}$AC长为半径画弧,两弧相交于点M、N,连接MN,与AC、BC分别交于点D、E,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 菱形的对角线互相平分 | B. | 正方形的对角线互相垂直平分 | ||
| C. | 矩形的对角线相等且平分 | D. | 等腰梯形的对角线相等且平分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD的边长为4,动点M、N同时从A点出发,点M沿AB以每秒1个单位长度的速度向中点B运动,点N沿折现ADC以每秒2个单位长度的速度向终点C运动,设运动时间为t秒,则△CMN的面积为S关于t函数的图象大致是( )
如图,正方形ABCD的边长为4,动点M、N同时从A点出发,点M沿AB以每秒1个单位长度的速度向中点B运动,点N沿折现ADC以每秒2个单位长度的速度向终点C运动,设运动时间为t秒,则△CMN的面积为S关于t函数的图象大致是( )| A. |  | B. | 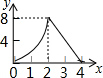 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ② | B. | ②④ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com