Question

19．如图，正方形ABCD的边长为4，动点M、N同时从A点出发，点M沿AB以每秒1个单位长度的速度向中点B运动，点N沿折现ADC以每秒2个单位长度的速度向终点C运动，设运动时间为t秒，则△CMN的面积为S关于t函数的图象大致是（　　）

• A．
• B．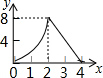
• C．
• D．

Answer 1

分析 当0≤t≤2时，AM=t，AN=2t，利用S=S_{正方形ABCD}-S_△AMN-S_△BCM-S_△CDN可得到S=-t²+6t；当2＜t≤4时，CN=8-2t，利用三角形面积公式可得S=-4t+16，于是可判断当0≤t≤2时，S关于t函数的图象为开口向上的抛物线的一部分，当2＜t≤4时，S关于t函数的图象为一次函数图象的一部分，然后利用此特征对四个选项进行判断．

解答 解：当0≤t≤2时，AM=t，AN=2t，
所以S=S_{正方形ABCD}-S_△AMN-S_△BCM-S_△CDN=4×4-$\frac{1}{2}$•t•2t-$\frac{1}{2}$•4•（4-t）-$\frac{1}{2}$•4•（4-2t）=-t²+6t；
当2＜t≤4时，CN=8-2t，S=$\frac{1}{2}$•（8-2t）•4=-4t+16，
即当0≤t≤2时，S关于t函数的图象为开口向下的抛物线的一部分，当2＜t≤4时，S关于t函数的图象为一次函数图象的一部分．
故选D．

点评 本题考查了动点问题的函数图象：函数图象是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．解决本题的关键是利用分类讨论的思想求出S与t的函数关系式．