
【题目】如图,△ABC是等边三角形,D是AC边上一点,E是BC延长线上一点,连接DE.
(1)如图1,若点D是AC中点,且DB=DE. 求证:AD=CE.
(2)如图2,若点D是AC边上任意一点,且DB=DE,则(1)中结论是否成立,如成立,请证明;如不成立,请说明理由.

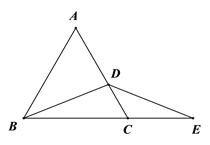
图1 图2
【答案】(1)证明见解析;
(2)结论成立,理由见解析.
【解析】试题分析:(1)求出∠E=∠CDE,推出CD=CE,根据等腰三角形性质求出AD=DC,即可得出答案;(2)过D作DF∥BC,交AB于F,证△BFD≌△DCE,推出DF=CE,证△ADF是等边三角形,推出AD=DF,即可得出答案.
试题解析:(1)证明:∵△ABC是等边三角形
∠ABC=∠ACB=60°
∵△ABC是等边三角形,点D为AC中点
∴BD平分∠ABC,AD =CD
∴∠DBC=![]() ∠ABC=
∠ABC=![]() ×60°=30°
×60°=30°
∵DB=DE
∴∠E=∠DBC=30°
又∵∠ACB是△DCE的外角
∴∠CDE=∠ACB-∠E=60°-30°=30°
∴∠CDE=∠E
∴CD=CE
∴CE=AD
(2) 过点D作DF∥BC交AB于F
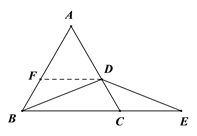
∵△ABC是等边三角形
∴∠A=∠ABC=∠ACB=60°,AB=AC
∵DF∥BC
∴∠AFD=∠ABC=60°,∠ADF=∠ACB=60°
即∠A=∠AFD=∠ADF
∴△AFD是等边三角形
∴AF=FD=AD
∴AB-AF=AC-AD
即BF=CD
∵DB=DE
∴∠E=∠DBC
∴∠ABC-∠DBC=∠ACB-∠E
即∠ABD=∠CDE
∴△FBD≌△CDE
∴CE=DF
∴CE=AD


科目:初中数学 来源: 题型:
【题目】某商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元,售出3件A种商品和5件B种商品所得利润为1100元;
(1)求每件A种商品和每件B种商品售出后所得利润各多少元?
(2)若该商场一次购进A、B两种商品共34件,全部售完后所得利润不低于4000元,那么该商场至少需要购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=![]() ∠CAB.
∠CAB.

(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=![]() ,求BC和BF的长.
,求BC和BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为促销,决定对A,B两种商品进行打折出售.打折前,买6件A商品和3件B商品需要54元,买3件A商品和4件B商品需要32元;打折后,买50件A商品和40件B商品仅需364元,这比打折前少花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
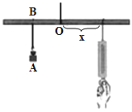
【题目】如图所示,小华设计了一个研究杠杆平衡条件的实验,在一根长为1000cm的匀质木杆的中点左侧固定位置B处悬挂重物A,在中点的右侧用一个弹簧秤向下拉,改变弹簧与点O的距离x(cm)观察弹簧的示数y(N)的变化情况,实验数据记录如下:
(1)观察数据,求出y(N)与x(cm)之间的函数关系式,写出自变量的取值范围;

(2)当弹簧秤的示数是24N时,弹簧与点O的距离是多少?随着弹簧秤与点O的距离不断减小,弹簧秤上的示数将发生怎样的变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有“G20,峰,会”3个球,这些球除标注外都相同,搅匀后从中任意摸出1个球,不放回,搅匀后再从中任意摸出1个球,不放回,再从中摸出最后1个球.
(1)请画树状图分析两次摸球情况;
(2)小明和小亮玩这个摸球游戏,小明摸到三个球的顺序依次为“G20、峰、会”,或“峰、会、G20”,小明胜,否则小亮胜.请判断该游戏对双方是否公平?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com