
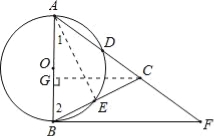
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=![]() ∠CAB.
∠CAB.

(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=![]() ,求BC和BF的长.
,求BC和BF的长.
【答案】(1)证明见解析;(2)BC=2![]() ,BF=
,BF=![]() .
.
【解析】
试题分析:(1)连接AE,利用直径所对的圆周角是直角,从而判定直角三角形,利用直角三角形两锐角相等得到直角,从而证明∠ABF=90°.(2)利用已知条件证得△AGC∽△ABF,利用比例式求得线段BC和BF的长.
试题解析:(1)证明:连接AE,在⊙O中,∵∠AEB=90°,∴∠1+∠2=90°.∵AB=AC,∴∠1= ∠CAB.
∵∠CBF= ∠CAB,∴∠1=∠CBF,∴∠CBF+∠2=90°,即∠ABF=90°,∴直线BF是⊙O的切线.(2)解:过点C作CG⊥AB于G.∵sin∠CBF=![]() ,∠1=∠CBF,∴sin∠1=
,∠1=∠CBF,∴sin∠1=![]() ,在Rt△AEB中,∠AEB=90°,∴BE=ABsin∠1=
,在Rt△AEB中,∠AEB=90°,∴BE=ABsin∠1=![]() ,∵AB=AC,∠AEB=90°,∴BC=2BE=2
,∵AB=AC,∠AEB=90°,∴BC=2BE=2![]() ,在Rt△ABE中,由勾股定理得AE=
,在Rt△ABE中,由勾股定理得AE=![]() ,∴sin∠2=
,∴sin∠2=![]() =
=![]() =
=![]() ,cos∠2=
,cos∠2=![]() =
=![]() =
=![]() ,在Rt△CBG中,可求得GC=4,GB=2,∴AG=3,∵GC∥BF,∴△AGC∽△ABF,∴
,在Rt△CBG中,可求得GC=4,GB=2,∴AG=3,∵GC∥BF,∴△AGC∽△ABF,∴![]() ,∴BF=
,∴BF=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
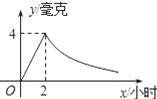
【题目】病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克,已知服药后,2小时前每毫升血液中的含药量y(毫克)与时间x(小时)成正比例,2小时后y与x成反比例(如图所示).根据以上信息解答下列问题.
(1)求当0≤x≤2时,y与x的函数关系式;
(2)求当x>2时,y与x的函数关系式;
(3)若每毫升血液中的含药量不低于2毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
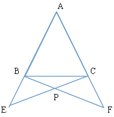
【题目】在△ABC中,AB=AC,点E,F分别在AB,AC的延长线上,AE=AF,BF与CE相交于点P,求证:PB=PC,并请直接写出图中其他相等的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100千米/小时,特快车的速度为150千米/小时,甲乙两地之间的距离为1000千米,两车同时出发,则图中折线大致表示两车之间的距离y(千米)与快车行驶时间t(小时)之间的函数图象是
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D是AC边上一点,E是BC延长线上一点,连接DE.
(1)如图1,若点D是AC中点,且DB=DE. 求证:AD=CE.
(2)如图2,若点D是AC边上任意一点,且DB=DE,则(1)中结论是否成立,如成立,请证明;如不成立,请说明理由.

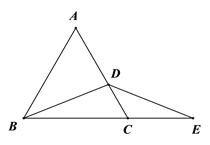
图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com