
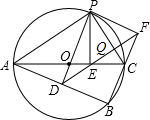
 如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交PC于点Q,同时交BC的延长线于F点,连接PF、PA.
如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交PC于点Q,同时交BC的延长线于F点,连接PF、PA.
|


科目:初中数学 来源: 题型:
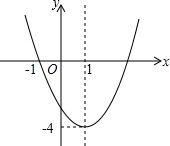 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( )| A、二次函数的图象关于直线x=1对称 |
| B、当x>1时,y随x的增大而减小 |
| C、-1和3是方程ax2+bx+c=0(a≠0)的两个根 |
| D、函数y=ax2+bx+c(a≠0)的最小值是-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
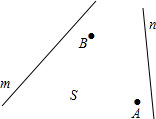 如图,某公司要在公路m,n之间的S区域修建一所物流中心P.按照设计要求,物流中心P到区域S内的两个社区A、B的距离必须相等,到两条公路m、n的距离也必须相等.那么物流中心P应建在什么位置才符合设计要求?请你在图中画出它的位置并标出所求.(保留画图痕迹)
如图,某公司要在公路m,n之间的S区域修建一所物流中心P.按照设计要求,物流中心P到区域S内的两个社区A、B的距离必须相等,到两条公路m、n的距离也必须相等.那么物流中心P应建在什么位置才符合设计要求?请你在图中画出它的位置并标出所求.(保留画图痕迹)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com