
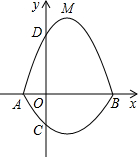 ��ͼ����ƽ��ֱ������ϵxOy�У�A��BΪx�������㣬C��DΪy���ϵ����㣬������A��C��B��������C1��һ�����뾭����A��D��B��������C2��һ������ϳ�һ��������ߣ����ǰ�����������߽��������ߡ�����֪��C������Ϊ��0��-$\frac{3}{2}$������M��������C2��y=-x2+2x+3�Ķ��㣮
��ͼ����ƽ��ֱ������ϵxOy�У�A��BΪx�������㣬C��DΪy���ϵ����㣬������A��C��B��������C1��һ�����뾭����A��D��B��������C2��һ������ϳ�һ��������ߣ����ǰ�����������߽��������ߡ�����֪��C������Ϊ��0��-$\frac{3}{2}$������M��������C2��y=-x2+2x+3�Ķ��㣮���� ��1���ڽ���ʽy=-x2+2x+3����y=0�������A��B���꣬�ٻ�Ϊ����ʽ�����M�����ꣻ
��2������A��B��C��������꣬�ɴ���ϵ���������C1�Ľ���ʽ��
��3�����ڣ����P������Ϊ��n��$\frac{1}{2}$n2-n-$\frac{3}{2}$������ɱ�ʾ����PBC������������ö��κ��������ʿ���������ֵ��
��� ��
��1����y=-x2+2x+3����y=0���ɵ�-x2+2x+3=0�����x1=-1��x2=3��
��A��-1��0����B��3��0����
��y=-x2+2x+3=-��x-1��2+4��
��M��1��4����
��2����C1����ʽΪy=ax2+bx+c��
��A��B��C�������������$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=-\frac{3}{2}}\end{array}\right.$�����$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-1}\\{c=-\frac{3}{2}}\end{array}\right.$��
��������C1����ʽΪy=$\frac{1}{2}$x2-x-$\frac{3}{2}$��
��3�����ڣ�
���P��������n��$\frac{1}{2}$n2-n-$\frac{3}{2}$����0��n��3����
��S��PBC=S��POC+S��BOP-S��BOC=$\frac{1}{2}$��$\frac{3}{2}$��n+$\frac{1}{2}$��3����-$\frac{1}{2}$n2+n+$\frac{3}{2}$��-$\frac{1}{2}$��3��$\frac{3}{2}$=-$\frac{3}{4}$��n-$\frac{3}{2}$��2+$\frac{27}{16}$��
��-$\frac{3}{4}$��0��
�൱n=$\frac{3}{2}$ʱ��S��PBC�����ֵ�����ֵ��$\frac{27}{16}$��
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ���������κ�������ֵ�������ε�������¶����֪ʶ���ڣ�1����ע�⺯��ͼ����������Ľ����������ʽ���ڣ�2����ע�����ϵ������Ӧ�ò��裬�ڣ�3������P�������ʾ����PBC��������Ӷ��õ����κ�������ʽ�ǽ���Ĺؼ������⿼��֪ʶ�㲻��̫�࣬�ۺ��Խ�ǿ�����ѶȲ���������÷֣�


 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
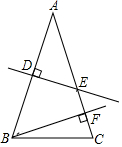
 ��ͼ����E=��F=90�㣬��B=��C��AE=AF���������н��ۣ��١�1=��2����BE=CF���ۡ�ACN�ա�ABM����CN=MB������ȷ�Ľ����Ǣ٢ڢۢܣ�������Ϊ��ȷ�Ľ�����Ŷ����ϣ�
��ͼ����E=��F=90�㣬��B=��C��AE=AF���������н��ۣ��١�1=��2����BE=CF���ۡ�ACN�ա�ABM����CN=MB������ȷ�Ľ����Ǣ٢ڢۢܣ�������Ϊ��ȷ�Ľ�����Ŷ����ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У�AB=AC��AB�Ĵ�ֱƽ���߽�AB��D����AC��E��EC�Ĵ�ֱƽ����ǡ�þ�����B�����A�Ķ�����
��ͼ����ABC�У�AB=AC��AB�Ĵ�ֱƽ���߽�AB��D����AC��E��EC�Ĵ�ֱƽ����ǡ�þ�����B�����A�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com