
 如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CN=MB其中正确的结论是①②③④(将你认为正确的结论序号都填上)
如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CN=MB其中正确的结论是①②③④(将你认为正确的结论序号都填上) 分析 利用全等三角形的判定和性质,可以证明△AEB≌△AFC,△AEM≌△AFN,△ACN≌△ABM,由此即可一一判断.
解答 解:在△AEB和△AFC中,
$\left\{\begin{array}{l}{∠E=∠F}\\{∠B=∠C}\\{AE=AF}\end{array}\right.$,
∴△AEB≌△AFC,
∴∠EAB=∠FAC,
∴∠1=∠2,BE=CF,AB=AC,故①②正确,
在△AEM和△AFN中,
$\left\{\begin{array}{l}{∠2=∠1}\\{AE=AF}\\{∠E=∠F}\end{array}\right.$,
∴△AEM≌△AFN,
∴AM=AF,∵AC=AB,
∴CM=BN,故④正确,
在△ACN和△ABM中,
$\left\{\begin{array}{l}{∠C=∠B}\\{∠CAN=∠BAM}\\{AN=AM}\end{array}\right.$,
∴△ACN≌△ABM,故③正确,
故答案为①②③④.
点评 本题考查全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
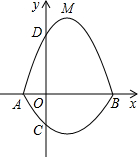 如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线C1的一部分与经过点A、D、B的抛物线C2的一部分组合成一条封闭曲线,我们把这条封闭曲线叫做“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=-x2+2x+3的顶点.
如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线C1的一部分与经过点A、D、B的抛物线C2的一部分组合成一条封闭曲线,我们把这条封闭曲线叫做“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=-x2+2x+3的顶点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com