
分析 (1)直接利用二次根式乘法运算法则求出答案;
(2)首先化简二次根式,进而利用二次根式除法运算法则求出答案;
(3)直接利用负整数指数幂的性质以及零指数幂的性质和绝对值的性质以及二次根式的性质分别化简求出答案;
(4)直接化简二次根式,进而合并求出答案.
解答 解:(1)$\sqrt{\frac{2}{3}}$×$\sqrt{12}$=$\sqrt{\frac{2}{3}×12}$=$\sqrt{8}$=2$\sqrt{2}$;
(2)($\sqrt{24}$-$\sqrt{\frac{1}{6}}$)÷$\sqrt{3}$
=(2$\sqrt{6}$-$\frac{\sqrt{6}}{6}$)÷$\sqrt{3}$
=$\frac{11\sqrt{6}}{6}$×$\frac{\sqrt{3}}{3}$
=$\frac{11\sqrt{2}}{6}$;
(3)($\frac{1}{2}$)-1×($\sqrt{3}$-$\sqrt{2}$)0+$\frac{4}{\sqrt{8}}$-|-$\sqrt{2}$|
=2×1+$\sqrt{2}$-$\sqrt{2}$
=2;
(4)$\frac{\sqrt{8}}{2}$+2$\sqrt{18}$-$\frac{1}{4}$$\sqrt{32}$
=$\sqrt{2}$+2×3$\sqrt{2}$-$\frac{1}{4}$×4$\sqrt{2}$
=7$\sqrt{2}$-$\sqrt{2}$
=6$\sqrt{2}$.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
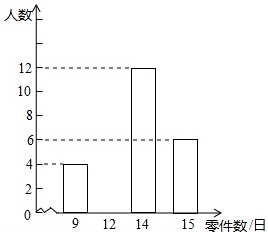 某车间有120名工人,为了了解这些工人日加工零件数的情况,随机抽出其中的30名工人调查,整理调查结果,绘制出不完整的条形统计图(如图).根据图中的信息,解答下列问题:
某车间有120名工人,为了了解这些工人日加工零件数的情况,随机抽出其中的30名工人调查,整理调查结果,绘制出不完整的条形统计图(如图).根据图中的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
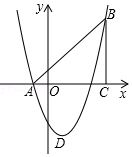 如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,OC=4,抛物线y=x2+bx+c经过A,B两点,抛物线的顶点为D.
如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,OC=4,抛物线y=x2+bx+c经过A,B两点,抛物线的顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CN=MB其中正确的结论是①②③④(将你认为正确的结论序号都填上)
如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CN=MB其中正确的结论是①②③④(将你认为正确的结论序号都填上)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com