
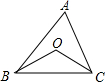
 如图,O是△ABC内任意一点,连接OB、OC.
如图,O是△ABC内任意一点,连接OB、OC.分析 (1)延长BO交AC于点D,首先利用三角形的外角性质得到∠BOC>∠ODC,让根据∠ODC>∠A,证得∠BOC>∠A;
(2)根据三角形的三边关系证得AB+AD>OB+OD,OD+CD>OC,从而得到AB+AD+CD>OB+OC,进而得到AB+AC>OB+OC.
解答 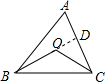 解:(1)证明:延长BO交AC于点D,
解:(1)证明:延长BO交AC于点D,
∴∠BOC>∠ODC,
又∠ODC>∠A,
∴∠BOC>∠A;
(2)AB+AC>OB+OC,
∵AB+AD>OB+OD,OD+CD>OC,
∴AB+AD+CD>OB+OC,
即:AB+AC>OB+OC.
点评 本题考出了三角形的三边关系及三角形的外角的性质,解题的关键是能够正确的构造三角形,难度不大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 12 | C. | 13 | D. | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解一批电视机的使用寿命 | |
| B. | 了解我市居民家庭一周内丢弃塑料袋的数量 | |
| C. | 了解我市中学生的近视率 | |
| D. | 了解我校学生最喜爱的体育项目 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “打开电视,正在播放《自然传奇》”是必然事件 | |
| B. | 想了解某种饮料中含色素的情况,应进行全面调查 | |
| C. | 数据1,1,2,2,3的众数是3 | |
| D. | 对报考空飞班的每个学生的身体情况必须进行全面调查 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com