
【题目】如图,经过原点的抛物线y=﹣x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B,点C不重合).连接CB,CP.
(1)当m=3时,求点A的坐标及BC的长;
(2)当m>1时,连接CA,问m为何值时CA⊥CP?
(3)当m>1时过点P作PE⊥PC且PE=PC,问是否存在m,使得点E落在坐标轴上?若存在,求出所有满足要求的m的值,并定出相对应的点E坐标;若不存在,请说明理由.
【答案】
(1)
解:当m=3时,y=﹣x2+6x=﹣x(x﹣6).
令y=0得:﹣x(x﹣6)=0,解得x=0或x=6,
∴点A的坐标为(6,0).
∴抛物线的对称轴为直线x=3.
∵B、C关于直线x=3对称,
∴BC=2×(3﹣1)=4
(2)
解:如图1所示:过点C作AH⊥x轴,垂足为H.

∵抛物线y=﹣x2+2mx的对称轴为x=m,
∴点B和点C直线x=m对称.
∵当x=1时,y=2m﹣1,
∴点B的坐标为(1,2m﹣1).
∴PB=m﹣1.
∵点B与点C关于直线x=m对称,
∴C(2m﹣1,2m﹣1).
∴BC=2m﹣2.
∴H(2m﹣1,0).
∴AH=1,CH=2m﹣1.
∵∠ACH=∠PCB=90°,
∴∠ACH=∠BCP.
又∵∠AHC=∠PCB=90°,
∴△ACH∽△PCB.
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴m= ![]()
(3)
解:当m>1时,BC=2(m﹣1),PM=m,BP=m﹣1.
①若点E在x轴上时,如图2所示:

∵∠CPE=90°,
∴∠MPE+∠BPC=∠MPE+∠MEP=90°,
∴∠BPC=∠MEP.
在△BPC和△MEP中,  ,
,
∴△BPC≌△MEP.
∴BC=PM.
∴2(m﹣1)=m,解得m=2,
∴E(2,0).
若点E在y轴上,如图3所示:过点P作PN⊥y轴与点N.

∵∠EPC=90°,
∴∠EPB+∠BPC=90°.
∵∠NPE+∠EPB=90°,∠NEP=∠EPB,
∴∠BPC=∠EPN.
在△EPN和△CPB中, 
∴△BPC≌△NPE.
∴BP=NP=OM=1,
∴m﹣1=1,
∴m=2
∴E(0,4).
综上所述,当m=2时,点E的坐标为(2,0)或(0,4)
【解析】(1)把m=3代入得到抛物线的解析式,然后令y=0得:﹣x(x﹣6)=0,从而可求得点A的坐标,利用抛物线的对称性可得到抛物线的对称轴为x=m,然后利用抛物线的对称性可得到BC的长;(2)过点C作AH⊥x轴,垂足为H.先求得点B和点C的坐标,由点B、点P和点C的坐标可得到PB、BC的长,然后由点C和点A的坐标可求得CH,AH的长,接下来,再证明△ACH∽△PCB,最后依据相似三角形的性质列方程求解即可;(3)当m>1时,BC=2(m﹣1),PM=m,BP=m﹣1.①若点E在x轴上时,先证明△BPC≌△MEP,依据全等三角形的性质可得到BC=PM,然后依据BC=PM可得到关于m的方程,从而可求得m的值,故此可得到E的坐标;②若点E在y轴上,过点P作PN⊥y轴与点N.然后证明△BPC≌△NPE,则BP=NP=OM=1,则m﹣1=1,可求得m=2,于是可求得点E的坐标.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:如图1,⊙O与直线a、b都相切,不论⊙O如何转动,直线a、b之间的距离始终保持不变(等于⊙O的直径),我们把具有这一特性的图形成为“等宽曲线”,图2是利用圆的这一特性的例子,将等直径的圆棍放在物体下面,通过圆棍滚动,用较小的力既可以推动物体前进,据说,古埃及人就是利用这样的方法将巨石推到金字塔顶的. 拓展应用:如图3所示的弧三角形(也称为莱洛三角形)也是“等宽曲线”,如图4,夹在平行线c,d之间的莱洛三角形无论怎么滚动,平行线间的距离始终不变,若直线c,d之间的距离等于2cm,则莱洛三角形的周长为cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017宁夏)在边长为2的等边三角形ABC中,P是BC边上任意一点,过点 P分别作 PM⊥A B,PN⊥AC,M、N分别为垂足. 
(1)求证:不论点P在BC边的何处时都有PM+PN的长恰好等于三角形ABC一边上的高;
(2)当BP的长为何值时,四边形AMPN的面积最大,并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的解析式为y=﹣ ![]() x2+bx+5.
x2+bx+5.
(1)当自变量 x≥2时,函数值y 随 x的增大而减少,求b 的取值范围;
(2)如图,若抛物线的图象经过点A(2,5),与x 轴交于点C,抛物线的对称轴与x 轴交于B.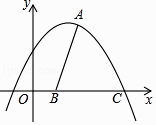
①求抛物线的解析式;
②在抛物线上是否存在点P,使得∠PAB=∠ABC?若存在,求出点P 的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某商场有一双向运行的自动扶梯,扶梯上行和下行的速度保持不变且相同,甲、乙两人同时站上了此扶梯的上行和下行端,甲站上上行扶梯的同时又以0.8m/s的速度往上跑,乙站上下行扶梯后则站立不动随扶梯下行,两人在途中相遇,甲到达扶梯顶端后立即乘坐下行扶梯,同时以0.8m/s的速度往下跑,而乙到达底端后则在原地等候甲.图2中线段OB、AB分别表示甲、乙两人在乘坐扶梯过程中,离扶梯底端的路程y(m)与所用时间x(s)之间的部分函数关系,结合图象解答下列问题: 
(1)求点B的坐标;
(2)求AB所在直线的函数表达式;
(3)乙到达扶梯底端后,还需等待多长时间,甲才到达扶梯底端?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,反比例函数y= ![]() 的图象与一次函数y=kx﹣3的图象在第一象限内相交于点A(4,m).
的图象与一次函数y=kx﹣3的图象在第一象限内相交于点A(4,m).
(1)求m的值及一次函数的解析式;
(2)若直线x=2与反比例和一次函数的图象分别交于点B、C,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4与x轴交于A(﹣2,0)、B(4、0)两点,与y轴交于C点.
(1)求抛物线的解析式;
(2)T是抛物线对称轴上的一点,且△ATC是以AC为底的等腰三角形,求点T的坐标;
(3)M、Q两点分别从A、B点以每秒1个单位长度的速度沿x轴同时出发相向而行,当点M到原点时,点Q立刻掉头并以每秒 ![]() 个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,过点M的直线l⊥x轴交AC或BC于点P.求点M的运动时间t与△APQ面积S的函数关系式,并求出S的最大值.
个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,过点M的直线l⊥x轴交AC或BC于点P.求点M的运动时间t与△APQ面积S的函数关系式,并求出S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解市民“获取新闻的最主要途径”某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图. 
根据以上信息解答下列问题:
(1)这次接受调查的市民总人数是;
(2)扇形统计图中,“电视”所对应的圆心角的度数是;
(3)请补全条形统计图;
(4)若该市约有80万人,请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com